As arestas e do tetraedro mede, respectivamente, e , e as medidas dos ângulos e , são (respectivamente) e . Calcule o volume do tetraedro em função de .
Passo 1
O que temos no enunciado é algo parecido com isso:
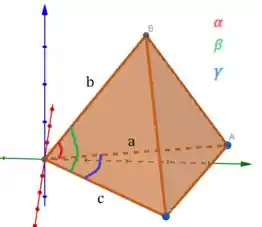
O volume desse tetraedro é , então vamos calcular isso aí haha
Passo 2
Temos:
Seja o ângulo que faz com :
Substituindo os tamanhos das arestas: