Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 23.Problemas - Ex. 1

Seja R :   R ²   →   R ² uma rotação em torno da origem. Use as equações que dão as coordenadas de R v   para mostrar que < R u ,   R v >   =   < u ,   v > e | R v |   =   | v | para quaisquer   u ,   v   ∈   R ² .

Passo 1

Olá galera! tudo bem?

Bora junto resolver mais um problema!

Este exercício é bem longo e vai requerer um pouco mais de domínio algébrico, já que o mesmo se trata de uma demonstração.

Preparado?

Então temos um operador descrito como R   :   R ²   →   R ² , que leva cada vetor v no vetor   R ( v ) que dele resulta pela rotação de ângulo θ em torno da origem.

Podemos observar a imagem abaixo e com ela perceber que R ( u + v )   =   R ( u )   + R ( v ) .

Assim como R ( α v )   =   α R v para v   ∈   R ²   e   α   ∈   R

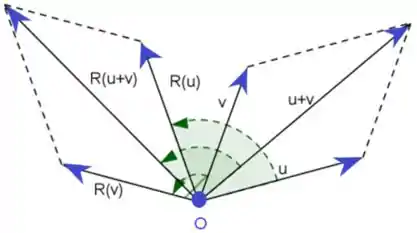
Para um vetor v   =   ( x ,   y )   ∈   R ² arbitrário, seja R ( v )   =   ( x '   ,   y '   ) . Sabemos que existe uma matriz A associada a transformação R , tal que R ( v )   =   ( A v t ) t   , temos que A   ∈   M ( 2   ×   2 ). Queremos então determinar a matriz:

a b c d = A

onde R ( e 1 )   =   ( a ,   c ) e R ( e 2 )   =   ( b , d ) , com e 1   =   ( 1,0 )   e   e 2   =   ( 0,1 ) .

Até aí tranquilo?

Calma a questão é chata mas tá quase acabando!

Passo 2

Sabendo das definições de seno e cosseno o vetor unitário R ( e 1 ) , que forma com e 1 um ângulo θ tem coordenadas c o s θ   e   s e n θ , ou seja, R ( e 1 )   =   ( c o s θ , s e n θ ) . Além disso, como e 2 forma com e 1 um ângulo reto, R ( e 2 ) também forma com R ( e 1 ) um ângulo reto.

Logo R ( e 2 )   =   ( - s e n θ ,   c o s θ )

Para melhor entender vamos focar na imagem abaixo:

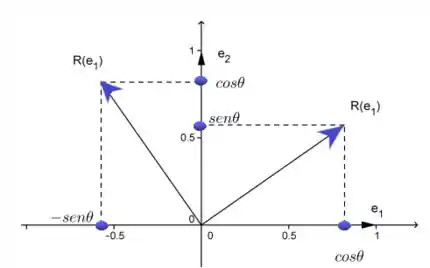
Portanto, a rotação R :   R ²   →   R ² leva um vetor v   =   ( x ,   y ) no vetor R ( v )   =   ( A v t ) t =   ( x '   ,   y '   ) .     Onde :

c o s θ - s e n θ s e n θ c o s θ = A

Logo teremos que:

A v t =   c o s θ - s e n θ s e n θ c o s θ   . x y = x c o s θ - y s e n θ x s e n θ + y c o s θ

Ou seja

x c o s θ - y s e n θ =   x ' x s e n θ + y c o s θ =   y '

A matriz de R relativa à base canônica de R ² é portanto a matriz A .

Prontinho, acabamos te vejo na próxima questão!

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Em cada parte, calcule p , q usando o produto interno do E x e m p l o7 . p = - 2 + x + 3 x 2 ,q = 4 - 7 x 2 p = - 5 + 2 x + x 2 ,q = 3 + 2 x - 4 x 2
Em cada parte, esboce o círculo unitário em R 2 usando o produto interno dado. u , v = 1 4 u 1 v 1 + 1 16 u 2 v 2 u , v = 2 u 1 v 1 + u 2 v 2
Sejam u = u 1 , u 2 e v = v 1 , v 2 . Em cada parte, mostre que a expressão é um produto interno em R 2 verificando a validade dos axiomas de produto interno. u , v = 3 u 1 v 1 + 5 u 2 v 2 u , v = 4 u
Suponha que u ,v e w sejam vetores tais que u , v = 2 , v , w = - 3 , u , w = 5 u = 1 , v = 2 , w = 7 Em cada parte, calcule a expressão. u + v , v + w 2 v - w , 3 u + 2 w u - v - 2 w , 4 u + v u + v
Mostre que vale a identidade dada com vetores de qualquer espaço com produto interno. u , v = 1 4 u + v 2 - 1 4 u - v 2