Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 3.Problemas propostos - Ex. 14d
Com base na Figura 3.14, calcular
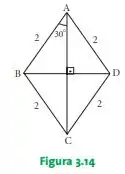
d)
Passo 1
Primeiro, vamos apresentar a intepretação gráfica:
Passo 2
O módulo do produto entre dois vetores pode ser encontrado por:
Porém, os vetores e são paralelos, logo, o ângulo formado entre eles é zero. Assim, temos:
Portanto, 😉
Resposta
Exercícios de Livros Relacionados
Ache o ângulo entre os seguintes pares de vetores: (c):3 i → + 3 j →e2 i → + j → - 2 k → ;
Se VxW = VxU e V ≠ 0 → , então W = U ?
(b)Mostre que se ( AxC )xB = 0 → , então AxBxC = AxBxC , ou seja, o produto vetorial é, neste caso, associativo.
(a)Prove que AxBxC + BxCxA + CxAxB = 0 ; Sugestão: Use o exercício anterior.
Sejam U = u 1 , u 2 , u 3 ,V = ( v 1 , v 2 , v 3 ) e W = w 1 , w 2 , w 3 . Prove a fórmula seguinte para o produto vetorial duplo UxVxW = U . W V - U . V W (b)Prove usando o item anterior e as proprie