Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 10.Exercício - Ex. 9
As bases , e estão representados na Figura 10-3. Quais delas são dextras e quais são sinistras?
Passo 1
O exercício fornceu várias bases e pede para dizermos quais são destras e quais são sinistras.
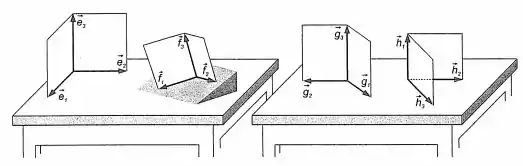
A base será dextra se respeitar a regra da mão direita e sinistra se respeitar a a da mão esquerda. Para isso, basta colocar o dedo indicador na direção do primeiro vetor, o dedo do meio na direção do segundo vetor e verificar se o dedão aponta na direção do terceiro vetor.
Passo 2
Para a base , vemos que a regra de mão direita se aplica. Portanto ela é dextra! O mesmo ocorre com a base .
Já para as bases e ocorre o contrário: a regra se aplica com a mão esquerda. Portanto elas são sinistras!
Resposta
Dextra: e .
Sinistra: e .
Exercícios de Livros Relacionados
Determinar m e n para que os conjuntos de vetores do R 3 dados abaixo sejam L.I. 3 ,5 m ,1 ,2 ,0 ,4 ,1 ,m ,3 { 1 ,3 ,5 ,2 ,m + 1 ,10 } { 6 ,2 ,n ,3 ,m + n ,m - 1 }
Mostrar que o conjunto { 1 , e x ,x e x } de vetores de C [ 0,1 ] é L.I.
Demonstrar que o conjunto { 1 , e x ,e 2 x } de vetores de C [ 0,1 ] é L.I.
Quais os subconjuntos abaixo do R 3 são linearmente independentes: 1,0 , 0 , 0,1 , 0 , 0,0 , 1 , 2,3 , 5 { 1,1 , 1 , 1,0 , 1 ,1,0 , - 2 } 0,0 , 0 ,1,2 , 3 ,4,1 , - 2 1,1 , 1 ,1,2 , 1 ,3,2 , - 1
Quais dos subconjuntos abaixo de P 4 ( R ) são linearmente independentes: 1 , x - 1 , x 2 + 2 x + 1 ,x 2 2 x ,x 2 + 1 ,x + 1 ,x 2 - 1 x x - 1 ,x 3 ,2 x 3 - x 2 ,x { x 4 + x - 1 , x 3 - x + 1 ,x 2 - 1