Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 7.Exercícios Suplementares - Ex. 9

Em cada caso, identifique o tipo de seção cônica representada pela equação.

Passo 1

Pois bem, para essa questão precisaremos nos lembrar das equações característica das principais cônicas que são: parábola, hipérbole, circunferência e elipse. No entanto, como em ambos os casos temos relação entre as variáveis e nenhum número ‘solto’ podemos desconfiar que as equações tratam de equações de parábolas.

Passo 2

Tomemos então a primeira equação e vamos trabalhar com ela

Essa equação é certamente de uma parábola que nos é bastante conhecida desde o ensino médio e que pode ser esboçada como sendo

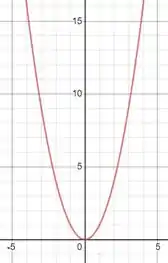
Passo 3

Procedendo de maneira igual para a segunda equação vamos ter

Essa equação também representa uma parábola, porém, a concavidade dela vai estar disposta de uma maneira diferente, podendo ser esboçada como

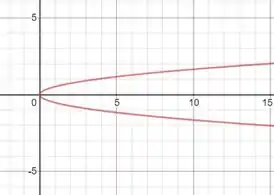
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre uma mudança de variáveis ortogonal que elimine os termos mistos da forma quadrática Q e expresse Q em termos das novas variáveis. Q = 3 x 1 2 + 4 x 2 2 + 5 x 3 2 + 4 x 1 x 2 - 4 x 2 x 3

Em cada caso, encontre uma mudança de variável ortogonal que elimine o termo misto da forma quadrática e expresse a forma quadrática em termos das variáveis novas. a - 3 x 1 2 + 5 x 2 2 + 5 x 1 x 2 b

Sejam A uma matriz simétrica n × n e q x = x T A x Onde x é um vetor qualquer em R n expresso em forma de coluna. O que pode ser dito sobre o valor de q se x for um autovetor unitário associado a um a

Suponha que a matriz hessiana de uma certa forma quadrática f x , y seja dada por H = 2 4 4 2 O que pode ser dito sobre a localização e a classificação dos pontos críticos de f?

Encontre, se houver, todos os pontos críticos de f e classifique-os como máximos relativos, mínimos relativos ou pontos de sela. f x , y = x 3 + y 3 - 3 x - 3 y