Exercícios de Classificação de Formas Quadráticas - Lista de Exercícios Resolvida

Determine por inspeção se é :

Classifique as formas quadráticas abaixo:

Seja . Para , o valor de :

É positivo ou negativo, dependendo de

É sempre negativo; independentemente de

É positivo ou zero, dependendo de

É sempre positivo; independente de

Considere as afirmativas:

1. Existe tal que
2. Existe tal que

1. (I) é verdadeira e (II) é falsa.
2. (I) é verdadeira e (II) é verdadeira.
3. (I) é falsa e (II) é falsa.
4. (I) é falsa e (II) é verdadeira.

Seja fixado um sistema de coordenadas no espaço, com uma

base ortonormal, e considere a quádrica de equação:

. Sabendo-se que , em que

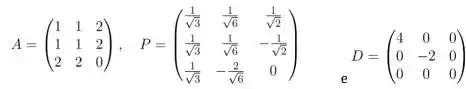
temos que uma equação reduzida para essa quádrica é:

Considere as afirmativas abaixo:

I - A equação não possui solução

II - A equação não possui solução

(a) Ambas são verdadeiras

(b) Ambas são falsas

(c) é verdadeira e é falsa

(d) é falsa e é verdadeira

Seja A uma matriz simétrica e a forma quadrática associada. Suponha que A não tenha autovalores nulos e que A possua pelo menos um autovalor positivo e um autovalor negativo. Então:

(a) Existem infinitos vetores x tais que

(b) Para todo x não nulo,

(c) Dependendo de A, pode existir ou não um vetor x não nulo tal que

(d) Para todo x não nulo,

Considere as afirmativas abaixo:

1. Existe tal que
2. Existe tal que

1. Ambas são verdadeiras
2. I é falsa e II é verdadeira
3. I é verdadeira e II é falsa
4. Ambas são falsas

Seja e . Considere a forma quadrática dada por e assinale a afirmativa VERDADEIRA

Existe tal que

Existem e tal que e

para todo

para todo

Seja . Para , o valor de :

é positivo, negativo, ou zero, dependendo de

é sempre positivo, independentemente de

é sempre negativo, independentemente de

é sempre negativo ou zero, independentemente de