Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.12 - Ex. 1
em cada parte determine se é uma matriz estocástica. Se não for estocástica, explique por que não é.
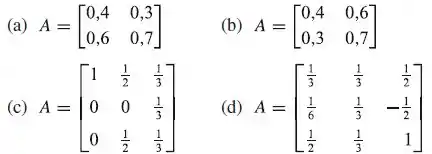
Passo 1
Para uma matriz ser estocástica, se somarmos os elementos coluna a soma total deles deve dar 1, por exemplo:
Para ser uma matriz estocástica, temos que e .
Também vale ressaltar que:
Sabendo disso temos:
Resposta
- É estocástica
- Não é, pois a soma dos itens da primeira coluna é e da segunda é .
- É estocástica
- Não é, pois o segundo item da terceira coluna assume valor negativo logo não pode ser probabilidade.
Exercícios de Livros Relacionados
Identifique a cônica e, quando for o caso, obtenha seus parâmetros geométricos ( a , b , c ou p ) e determine, em relação ao sistema inicial, os elementos geométricos principais: centro, focos, vértic
Identifique a cônica e, quando for o caso, obtenha seus parâmetros geométricos ( a , b , c ou p ) e determine, em relação ao sistema inicial, os elementos geométricos principais: centro, focos, vértic
Identifique a cônica e, quando for o caso, obtenha seus parâmetros geométricos ( a , b , c ou p ) e determine, em relação ao sistema inicial, os elementos geométricos principais: centro, focos, vértic
Identifique a cônica e, quando for o caso, obtenha seus parâmetros geométricos ( a , b , c ou p ) e determine, em relação ao sistema inicial, os elementos geométricos principais: centro, focos, vértic
Identifique a cônica e, quando for o caso, obtenha seus parâmetros geométricos ( a , b , c ou p ) e determine, em relação ao sistema inicial, os elementos geométricos principais: centro, focos, vértic