Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 6.1 - Ex. 21

Em cada parte, esboce o círculo unitário em R 2 usando o produto interno dado.

  1. u , v = 1 4 u 1 v 1 + 1 16 u 2 v 2
  2. u , v = 2 u 1 v 1 + u 2 v 2

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Temos que:

u , v = 1 4 u 1 v 1 + 1 16 u 2 v 2

Portanto:

u , u = 1 4 u 1 2 + 1 16 u 2 2

O círculo unitário é dado por u = 1 ou u 2 = 1

Sabendo que:

u = u , u 1 2

Temos que:

1 4 u 1 2 + 1 16 u 2 2 = 1

Se considerarmos que:

u = x , y

Temos que:

x 2 4 + y 2 16 = 1

Temos então o seguinte esboço:

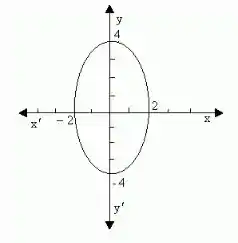
Passo 2

Para o item b temos que:

u , v = 2 u 1 v 1 + u 2 v 2

Portanto:

u , u = 2 u 1 2 + u 2 2

O círculo unitário é dado por:

u = 1

u 2 = 1

Sabendo que:

u = u , v 1 2

Logo:

2 u 1 2 + u 2 2 = 1

Se:

u = x , y

Temos que:

2 x 2 + y 2 = 1

Ou:

x 2 2 / 2 2 + y 2 1 = 1

Portanto, o círculo unitário é uma elipse com o eixo principal de comprimento 2 e o eixo menor de comprimento 2 .

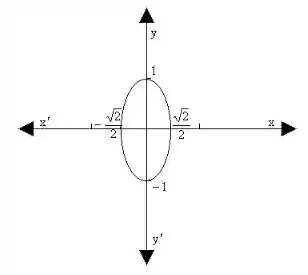
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine uma base ortonormal (em relação ao produto interno canônico) para o seguinte subespaço de R 3 : V = { x , y , z ∈ R 3 ; x - y + z = 0 }
Seja V = R 2 . Sejam v 1 = ( x 1 , y 1 ) e v 2 = x 2 , y 2 . Se f v 1 ,v 2 = 2 x 1 x 2 + x 1 y 2 + x 2 y 1 + y 1 y 2 , mostre que f é um produto interno.
Mostre a desigualdade triangular. (Veja 8.3.2 - iv) (Sugestão: v + w 2 = v + w , v + w ); desenvolva e use a desigualdade de Schwarz – 8.3.2 – iii).
Seja β = { 1,1 , 0 , 1,0 , 1 , ( 0,2 , 0 ) } . Ache uma base ortonormal β ' de R 3 em relação ao produto interno usual.
Seja W ⊂ R 3 o subespaço gerado por ( 1,0 , 1 ) e ( 1,1 , 0 ) .Considere W ⊥ em relação ao produto interno canônico. Encontre uma base para W ⊥ .A mesma pergunta anterior se W ⊥ é considerado em relaç