Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 7.1.Problemas Propostos - Ex. 1
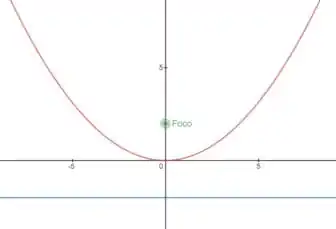
Em cada um dos problemas 1 a 18, estabelecer a equação de cada uma das parábolas, sabendo que:
1) vértice: ; diretriz:
Passo 1
Como a nossa diretriz é a reta e o nosso vértice está em , temos que o nosso foco está em
Pois é simétrico à diretriz em relação à parábola ok? Hehe
Bom, dada essa simetria, temos que um ponto da parábola deve ter a mesma distância até o foco e até a reta diretriz. Dado que o foco é e um ponto da reta diretriz é , vamos usar a fórmula de distância entre pontos:
Então, a equação da parábola é
Resposta
Exercícios de Livros Relacionados
Nos Exercícios de 33 a 40, ache uma equação da parábola com as propriedades dadas. Faça um esboço do gráfico.40. Os extremos do latus rectum são ( 1 ,3 ) e ( 7 ,3 ) .
Nos Exercícios de 33 a 40, ache uma equação da parábola com as propriedades dadas. Faça um esboço do gráfico.37. Vértice em ( 3 ,- 2 ) ; eixo x = 3 ; comprimento do latus rectum é 6.
50. Se uma parábola tiver seu foco na origem e o eixo x como eixo, prove que ela deve ter uma equação da forma y 2 = 4 k x + 4 k 2 ,k ≠ 0 .
52. Mostre que após uma translação de eixos para a nova origem - 1 4 π ,1 a equação y = 1 2 s e nx + cos x + 1 torna – se y ' = s e nx '
48. Na Figura 16, prove que α = β . (Sugestão: escolha os eixos coordenados de tal forma que a parábola tenha seu vértice na origem e seu eixo ao longo do eixo y e que se abra para cima. Seja Q a inte