Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 7.1.Problemas Propostos - Ex. 4
Em cada um dos problemas 1 a 18, estabelecer a equação de cada uma das parábolas, sabendo que:
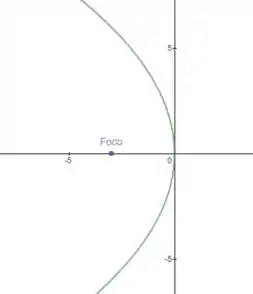
4) vértice: ; foco:
Passo 1
Como o vértice da parábola está em e o seu foco está em , ou seja, o foco “andou” ao longo do eixo , então nossa parábola está ao longo do eixo hehe
Bom, sabemos que a equação de uma parábola ao longo do eixo é
Sabemos também que o foco tem coordenadas
Dessa forma:
Então, a equação da nossa parábola é
Resposta
Exercícios de Livros Relacionados
49. A equação da diretriz de uma parábola é x + y = 0 e se foco está no ponto ( 1 ,1 ) . Ache (a) a equação do eixo da parábola, (b) as coordenadas do vértice e (c) 0 comprimento do latus rectum.
46. Suponha que a órbita de determinado cometa seja uma parábola com o Sol no foco. Quando o cometa está a 100 milhões de quilômetros do Sol, o ângulo entre o eixo da parábola e a reta do Sol até o co
54. Usando os resultados dos Exercícios 51 e 52 como referência, determine uma translação de eixos tal que a equação y = 1 2 3 s e nx + cos x + 2 torne – se y ' = s e nx ' .
53. Usando os resultados dos Exercícios 51 e 52 como referência, determine uma translação de eixos tal que a equação y = 1 2 s e nx - cos x - 3 torne – se y ' = s e nx ' .
Obtenha um vetor tangente, um vetor normal, e equações das retas tangente e normal à parábola P : x 2 = 4 p y no ponto T = h , k .