Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.1 - Ex. 46
46. Suponha que a órbita de determinado cometa seja uma parábola com o Sol no foco. Quando o cometa está a 100 milhões de quilômetros do Sol, o ângulo entre o eixo da parábola e a reta do Sol até o cometa é de 45°. Use o resultado do Exercício 45 para determinar a menor distância entre o cometa e o Sol.
Passo 1
Primeiro vamos escrever 100 milhões de forma mais bonita que é:
Agora, vamos lembrar da definição da parábola, que diz:
“A parábola é uma curva plana cujos pontos P são equidistantes a uma reta diretriz e a um ponto fixo F.”
Assim se o cometa está a Km do Sol que é nosso foco ela também tem a mesma distância da reta diretriz.
A menor distancia entre o cometa e o sol que é pedido no enunciado, acontece quando o cometa estiver no vértice da parábola, que foi demonstrado no exercício 45.
Passo 2
Abaixo tem uma figura que mostra mais ou menos nossa situação.
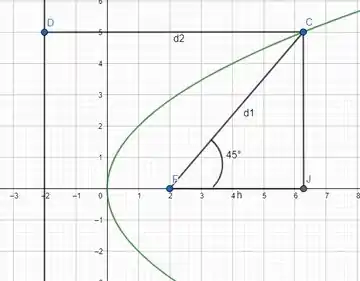
O ponto F é o foco que no caso é o Sol, o Ponto C é o cometa. O comprimento da reta d1 é igual ao comprimento da reta d2 pela definição da parábola.
Para resolver o problema precisamos achar a distância do foco até o vértice. Primeiro analisando nossa figura, vemos que a distância da reta diretriz até o ponto J é igual a d2.
Se descobrirmos a distância do foco até o ponto J podemos subtrair esse valor de d2 e descobrir a distância entre o foco e a reta diretriz, assim basta lembrar que o vértice é o ponto médio entre os dois.
Passo 3
Vamos achar a distância de F até J (chamando esse seguimento de h) por trigonometria, da seguinte forma:
Agora subtraindo esse valor de d2, obtemos:
Esse resultado representa a distância entre o foco e a reta diretriz, para achar a distância até o vértice basta dividir esse resultado por 2, assim:
Resposta
A menor distância entre o cometa e o Sol é dado por: