49. A equação da diretriz de uma parábola é e se foco está no ponto . Ache (a) a equação do eixo da parábola, (b) as coordenadas do vértice e (c) 0 comprimento do latus rectum.
Passo 1
Primeiro vamos visualizar o que temos através da figura a seguir:
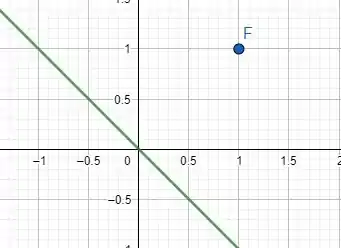
A reta em verde é a nossa reta diretriz e o ponto F é o nosso foco.
Passo 2
Para acharmos a equação do eixo, devemos lembrar que o eixo de uma parábola passa pelo foco e é perpendicular a reta diretriz. Em nossa figura ele fica assim:
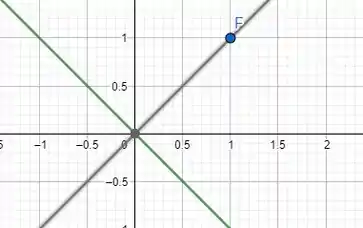
A equação que representa essa reta é:
Passo 3
Para achar as coordenadas do vértice, temos que lembrar que o vértice é o ponto médio entre o foco e a reta diretriz, e como a distância entre esses dois vale 2p, a distancia entre o foco e vértice vale p.
Para achar p basta calcular a distância entre o foco e a reta diretriz, da seguinte maneira:
Onde a, b e c são os coeficientes da equação da reta e x0 e y0 são as coordenadas do ponto, assim:
Assim a distância entre o foco e o vértice vale:
Agora usando a fórmula da distância entre dois pontos que tem a seguinte forma:
Aplicando o que temos:
Como o vértice tem que pertencer a reta do eixo da parábola, temos que:
Assim:
Resolvendo essa equação do segundo grau vemos que , então também é igual .
Logo nosso vértice tem coordenadas:
Passo 4
O comprimento do latus rectum é igual , então:
Descobrimos então que o comprimento do latus rectum vale .
Resposta
- O comprimento do latus rectum é igual a