Em cada um dos Problemas de 20 a 27, obter uma equação da elipse que satisfaça as condições dadas.
Centro , um foco e excentricidade
Passo 1
Vamos começar lembrando como é a fórmula da elipse:
Certo? Nãããão! Isso só rola quando o centro é em no centro, a fórmula da elipse com centro sem ser em é assim
Show, o pontos e são o centro que no caso são 1 e 4, então nossa formula fica assim:
O enunciado nos diz que temos um foco em e a excentricidade
Temos que , sendo nossa distancia focal, temos que , já que o foco está em e esté alinhado com o centro em .
Passo 2
Agora para achar vamos lembrar da nossa elipse e a relação entre e
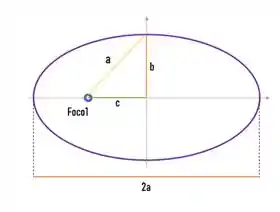
Então temos que
Então, nossa formula da elipse fica
Passo 3
Podemos ajeitar a resposta para ficar igual ao gabarito assim
Fazendo o MMC, temos que o denominador será 180, então ficamos com
Ajeitando isso ai ficamos com