Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 7.3.Problemas Propostos - Ex. 30

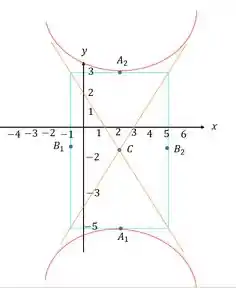
Em cada um dos problemas 25 a 30, determinar o centro, os vértices, os focos e a excentricidade das hipérboles dadas. Esboçe o gráfico.

16 x 2 - 9 y 2 - 64 x - 18 y + 199 = 0

Passo 1

Vamos começar fazendo uma análise do que o problema pede. O exercício que o esboço do gráfico, certo? Para isso precisamos encontrar a ,   b ,   c   A 1 , A 2 , C , F 1 , F 2 ,   B 1 ,   B 2 e com eles montar o gráfico. Bora la?

Primeiro faremos uma análise da equação dada:

16 x 2 - 9 y 2 - 64 x - 18 y + 199 = 0

Juntando os termos em comum:

16 x 2 - 64 x - 9 y 2 - 18 y = - 199

Podemos isolar termos, para isolar x   e y temos que deixar um positivo e outro negativo :

16 x 2 - 4 x - 9 y 2 + 2 y = - 199

Agora, podemos usar a regra para completar quadrados:

a ± b 2 = a 2 ± 2 a b + b 2

Então, podemos chamar 4 2 = b x e 2 2 = b y :

16 x 2 - 4 x + 2 2 - 16 . 2 2 - 9 y 2 + 2 y + 1 2 - 9 - 1 2 = - 199

Aplicando a propriedade distributiva:

16 x - 2 2 - 64 - 9 y + 1 2 + 9 = - 199

16 x - 2 2 - 9 y + 1 2 = - 199 + 64 - 9

16 x - 2 2 - 9 y + 1 2 = - 1 44

Dividindo tudo por -144:

16 x - 2 2 - 144 - 9 y + 1 2 - 144 = - 144 - 144

Simplificando:

- x - 2 2 9 + y + 1 2 16 = 1

Passo 2

Conseguimos chegar na seguinte equação:

- x - 2 2 9 + y + 1 2 16 = 1

y + 1 2 16 - x - 2 2 9 = 1

Lembrando que a equação é dada por:

y - k 2 a 2 - x - h 2 b 2 = 1

Isso significa que:

h = 2

k = - 1

a 2 = 16

a = 4

b 2 = 9

b = 3

Com essas informações podemos calcular os demais termos, primeiro com c :

c 2 = b 2 + a 2

c 2 = 9 + 16

c 2 = 25

c = 25 = 5

Passo 3

Com isso, conseguimos determinar alguns pontos importantes. Se C ( h , k ) , então:

C = ( 2 , - 1 )

Sabemos também que:

A 1 = ( h , k - a )

A 2 = ( h , k + a )

Então:

A 1 = 2 , - 1 - 4 = ( 2 , - 5 )

A 2 = ( 2 , 3 )

Agora, podemos calcular os focos:

F 1 = h , k - c = ( 2 , - 6 )

F 2 = h , k + c = ( 2,4 )

Por fim, calculamos as coordenadas B :

B 1 = h - b , k = ( - 1 , - 1 )

B 2 = h + b , k = ( 5 , - 1 )

e = c a = 5 4

Passo 4

Com todas as coordenadas calculadas, podemos esboçar um gráfico. Dica: colocamos dentro de um gráfico os eixos x e y . Depois acrescentamos as coordenadas A 1 , A 2 , B 2 , B 2 e o centro C . Cruzaremos assíntotas com centro C e entre as assíntotas teremos nosso esboço:

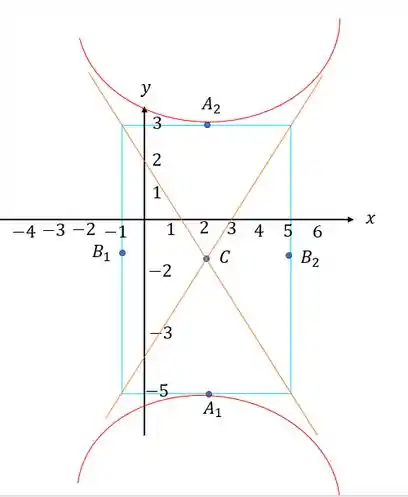
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as cônicas representadas pelas equações abaixo, encontrando também seus focos, diretrizes e excentricidade. 9 x 2 - 18 y 2 + 54 x - 36 = 0
Esboce o gráfico das cônicas a seguir, determinando seus focos, diretrizes e excentricidade. x 2 25 + y 2 9 = 1
Esboce o gráfico das cônicas a seguir, determinando seus focos, diretrizes e excentricidade. x 2 - y 2 = 4
Mostre que qualquer que seja o ponto P x ,y sobre a elipse dada no exercício 1 c , a soma das distancias deste ponto aos dois focos é igual a 10 .
Determine as cônicas representadas pelas equações abaixo, encontrando também seus focos, diretrizes e excentricidade. x = 4 y 2 - 16 y + 16