Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 11.7.2 - Ex. 2c
Determine as cônicas representadas pelas equações abaixo, encontrando também seus focos, diretrizes e excentricidade.
Passo 1
Temos um termo linear de na nossa equação, precisamos completar o quadrado e ficar com algo do tipo que podemos reescrever como e teremos uma cônica de origem . Vamos começar colocando em evidência e ir fazendo uma álgebra pra chegar no que queremos.
Repare que já está na forma que queremos! . Dando uma ajeitada:
Temos uma parábola que cresce na direção do eixo e está deslocada no eixo . Temos também que . Como , a parábola cresce na direção positiva de .
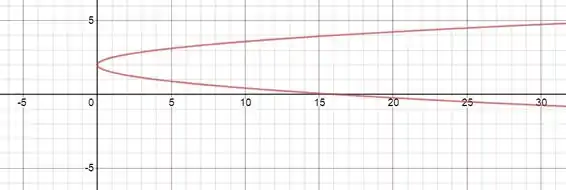
Passo 2
Seu gráfico é o seguinte:
Passo 3
Seu foco é em , ou seja:
Sua diretriz é a reta .
Lembre-se que o conceito de excentricidade não se aplica à parábola!
Resposta
Exercícios de Livros Relacionados
Ache o volume do sólido gerado pela rotação em torno do eixo x, da região limitada pela hipérbole x 2 a 2 - y 2 b 2 = 1 e pela reta x = 2 a .
Os focos de uma hipérbole estão em 2 ,7 e 2 ,- 7 , e a distância entre os vértices é 8 3 . Ache (a) a equação da hipérbole e (b) a equação das assíntotas.
Na figura 11, prove que α = β . (Sugestão: escolha os eixos coordenados de tal forma que o centro da hipérbole esteja na origem e os eixos da hipérbole estejam ao longo dos eixos coordenados. Então pr
37) Três postos de escuta estão localizados nos pontos A ( 0,0 ) , B ( 0 , 21 4 ) ,C ( 25 3 , 0 ) , a unidade de comprimento é o quilômetro. Microfones localizados nesses pontos mostram que uma arma e
38) Duas estações LORAN (abreviatura de Long-Range Navigation – Navegação de Longa Distância) A e B estão numa reta que vai de leste para oeste e A está a 80 km a leste de B. Um avião viaja para o les