Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 11.7.2 - Ex. 2b

Determine as cônicas representadas pelas equações abaixo, encontrando também seus focos, diretrizes e excentricidade.

9 x 2 - 18 y 2 + 54 x - 36 = 0

Passo 1

Temos um termo linear de x na nossa equação, precisamos completar o quadrado e ficar com algo do tipo x 2 + 2 x o x + x o 2 que podemos reescrever como x + x o 2 e teremos uma cônica de origem x o ,   0 . Vamos começar colocando 9 em evidência e ir fazendo uma álgebra pra chegar no que queremos.

9 x 2 + 6 x - 4 - 18 y 2 = 0

Do termo que acompanha o x dentro dos parênteses já sabemos que: 6 = 2 x o → x o = 3

Passo 2

Agora queremos fazer com que o valor independente dentro do parêntese seja x o 2 = 9 . Para isso temos que somar um valor 9 s de ambos os lados da equação de tal forma que:

- 4 + s = 9

Daí:

s = 13

E ficamos com:

9 x 2 + 6 x + 9 - 18 y 2 = 117

Agora sim! Podemos reescrever:

9 x + 3 2 - 18 y 2 = 117

Na forma canônica:

x + 3 2 13 - y 2 13 2 = 1

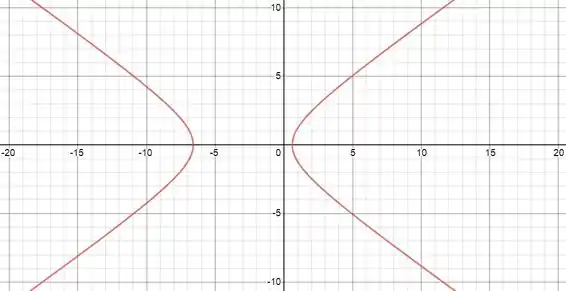
Temos uma hipérbole centrada em - 3 ,   0 !

Passo 3

Fazendo o gráfico dessa figura:

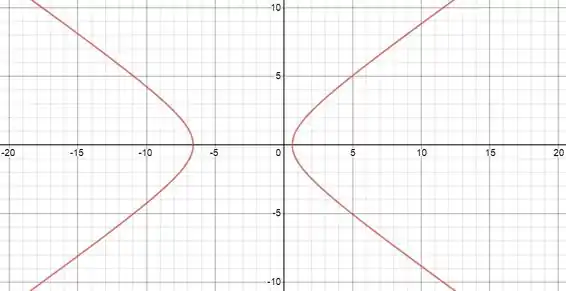
Passo 4

Agora vamos calcular os parâmetros dessa hipérbole:

Seu foco será em F 1 = x 0 - c ,   0 ; F 2 = ( x 0 + c , 0 ) .

c = a 2 + b 2 = 13 2 + 13 2 2 = 13 5 2 ≈ 14.53

Daí os focos ficaram em - 16 ,   0 ; 10 ,   0

Suas retas diretrizes serão:

x 1 = - a e + x o ; x 2 = a e + x o

x 1 = - 13 14.53 - 3 → x 1 = - 3.89

x 2 = 13 14.53 - 3 → x 2 = - 2.11

E pra finalizar, temos a excentricidade:

e = c a = 14.53 13 = 1.18

Resposta

c = 14.53

x 1 = - 3.89 ;   x 2 = - 2.11

e = 1.18

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o centro, os vértices, os focos e as equações das assíntotas da hipérbole dada. Faça um esboço da curva e de suas assíntotas e mostre os focos. 3 y 2 - 4 x 2 - 8 x - 24 y - 40 = 0
Ache o centro, os vértices, os focos e as equações das assíntotas da hipérbole dada. Faça um esboço da curva e de suas assíntotas e mostre os focos. 4 y 2 - 9 x 2 + 16 y + 18 x = 29
Ache o centro, os vértices, os focos e as equações das assíntotas da hipérbole dada. Faça um esboço da curva e de suas assíntotas e mostre os focos. y 2 - x 2 + 2 y - 2 x - 1 = 0
Ache o centro, os vértices, os focos e as equações das assíntotas da hipérbole dada. Faça um esboço da curva e de suas assíntotas e mostre os focos. 4 x 2 - y 2 + 56 x + 2 y + 195 = 0
Ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.Focos em ( 0,5 ) e ( 0 ,- 5 ) e um vértice ( 0 ,4 ) .