Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Hipérbole - Ex. 41

Em cada um dos problemas 38 a 43, determinar a equação reduzida, o centro, os vértices, os focos, a excentricidade e equações das assíntotas das hipérboles dadas. Esboçar o gráfico.

4 x 2 - y 2 - 32 x + 4 y + 24 = 0

Passo 1

E aí, tudo joinha?

Bora resolver mais essa?

Seguinte, nos deram essa equação geral:

4 x 2 - y 2 - 32 x + 4 y + 24 = 0

E nos pediram a equação reduzida dela, que é de uma dessas formas aqui:

x - h 2 a 2 - y - k 2 b 2 = 1

o u

y - k 2 a 2 - x - h 2 b 2 = 1

Onde ( h , k ) é o centro, beleza?

Vamos lá então...

Passo 2

A gente tem que completar os quadrados na equação, então é o seguinte:

4 x 2 - 8 x - 1 y 2 - 4 y = - 24

4 x 2 - 8 x + 16 ⏟ - 16 - y 2 - 4 y + 4 ⏟ - 4 = - 24

4 x - 4 2 - 64 - y - 2 2 + 4 = - 24

4 x - 4 2 - y - 2 2 = - 24 + 64 - 4

4 x - 4 2 - y - 2 2 = 36

x - 4 2 9 - y - 2 2 36 = 1

Prontinho! Chegamos à equação reduzida da hipérbole!

Passo 3

Agora a gente tem que achar os centros, os vértices, os focos, a excentricidade e as assíntotas...

Bom, pela equação ali a gente tira que a = 3 ,   b = 6 e podemos achar o c utilizando a relação:

c 2 = 9 + 36

c 2 = 45

c = 45 = 3   5

Vemos também que a nossa hipérbole tem eixo real paralelo ao eixo x (a parte que tá positiva), então os vértices são determinados andando a unidades em x a partir do centro.

Aliás, o centro ali é C = ( 4,2 ) , certinho?

Passo 4

Vamos continuar então...

Os vértices são:

A 1 1,2     e     A 2 ( 7,2 )

Pra achar os focos a gente anda c   unidades a partir do centro:

F 1 4 - 3 5 ,   2     e       F 2 ( 4 + 3 5 ,   2 )

E excentricidade é e = c a , então:

e = 3 5 3 = 5

Falta achar as assíntotas, pra isso, a gente pode pegar nossa equação reduzida e igualar a zero:

x - 4 2 9 - y - 2 2 36 = 0

Aí aqui a gente vai desenvolver essa expressão:

4 x - 4 2 36 - y - 2 2 36 = 0

4 x - 4 2 = y - 2 2

x - 4 2 = y - 2 2 4

x - 4 = ± y - 2 2 4

Então nossas assíntotas são:

x - 4 = y - 2 2 → 2 x - y - 6 = 0

x - 4 =   - y - 2 2 → 2 x + y - 10 = 0

Ufaaa! Todos os elementos da hipérbole foram encontrados! 😉

Passo 5

E pra encerrar com chave de ouro, o esboço do gráfico:

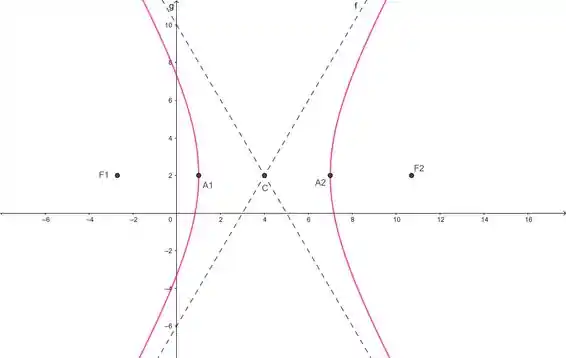
Resposta

Equação reduzida:   x - 4 2 9 - y - 2 2 36 = 1

Centro: ( 4,2 )

Vértices:   A 1 1,2     e     A 2 ( 7,2 )

Focos:   F 1 4 - 3 5 ,   2     e       F 2 ( 4 + 3 5 ,   2 )

Excentricidade:   e = 5

Assíntotas: 2 x - y - 6 = 0     e     2 x + y - 10 = 0    

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

( a ) O paralelogramo A B C D tem os lados A B e D C paralelos ao eixo transverso da hipérbole H : x 2 3 - y 2 2 = 1 e os lados A D e B C contidos em retas tangentes a H . Os pontos de tangência têm c
Prove que, se r é uma reta tangente a hipérbole H , então todos os seus pontos, exceto o ponto de tangência, pertencem a região côncava determinada por H .
( a ) O paralelogramo A B C D tem os lados A B e D C paralelos ao eixo transverso da hipérbole H : x 2 3 - y 2 2 = 1 e os lados A D e B C contidos em retas tangentes a H . Os pontos de tangência têm c
Sejam H : x 2 a 2 - y 2 b 2 = 1 , θ um número do intervalo [ 0 , π [ , α = a 2 s e n 2 θ - b 2 cos 2 ⁡ θ , e u → = ( cos ⁡ θ , s e nθ ) . ( a ) Prove que, se α0 , qualquer reta r paralela a u → é seca
Sejam P e Q pontos distintos, pertencentes a uma hipérbole H . Prove que as retas tangentes a H em P e Q são paralelas se, e somente se, o centro da hipérbole é o ponto médio de P Q .