Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 11.Problemas - Ex. 2a
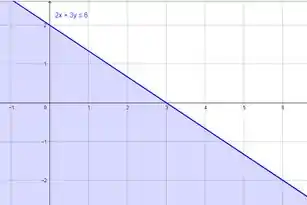
Para cada uma das regiões do plano descritas a seguir, escreva uma desigualdade ou sistema de desigualdades que a defina:
a) O semi-plano abaixo da reta 2x + 3y − 6 = 0.
Passo 1
Salve galera estudiosa, tudo certin?? É hora da resolução!!! Vamos lá??
Primeiramente, por definição, um semi-plano originado por uma reta tem duas possibilidades de desigualdade:
Manipulando a nossa reta dada no problema, temos que:
Como desejamos que o semiplano esteja abaixo da reta, basta que a nossa desigualdade siga o caso em que .
Logo, temos que:
Visualmente, teríamos a região representada no gráfico a seguir:
Resposta
Exercícios de Livros Relacionados
Sejam AB e CD retas paralelas. Ache uma equação para o plano determinado por elas.
Dados os pontos A=( 1 ,1 ,2 ) ,B=( 1 ,2 ,3 )eC=( - 1 ,2 ,1 ) , obtenha as coordenadas de um ponto P tal que o segmento O P seja perpendicular ao plano A B C . Use as coordenadas de P para achar uma eq
Obtenha uma equação para o plano que contém o ponto P e é perpendicular ao segmento de reta A B nos seguintes casos: a )P=( 0 ,0 ,0 ) ,A=( 1 ,2 ,3 ) ,B=( 2 ,- 1 ,2 ) ; b )P=( 1 ,1 ,- 1 ) ,A=( 3 ,5 ,2
Qual é o simétrico do ponto P=( 3 ,7 ,0 ) em relação ao plano x+2 y-z=5 ?
Existe um plano que passa pela origem e contém o ponto P=( x + 2 y + 3 z ,- 2 x +y-z ,- x+8 y+7 z ) , sejam quais forem os valores atribuídos a x ,yez . Ache a equação desse plano.