Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 128
Calcule a área do losango cujos vértices são os focos e as extremidades do eixo menor da elipse de equação . Em que condições esse losango é um quadrado?
Passo 1
Um losango é a figura plana onde os quatro lados são congruentes, e as diagonais são perpendiculares.
Se as medidas das diagonais medem, respectivamente, e , então a área do losango será:
No caso da questão, podemos fazer a seguinte construção:
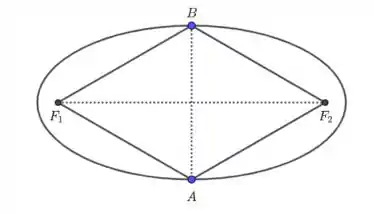
onde e são os focos e são as extremidades do eixo menor.
Passo 2
A área do losango será:
Sabemos que
Logo, a área será
Passo 3
Quando o losango será um quadrado? Um quadrado é um caso especial de losango quando as diagonais são iguais. Assim, devemos ter
Assim,
Portanto, o losango será um quadrado quando .
Resposta
A área mede e será um quadrado quando .
Exercícios de Livros Relacionados
Mostre que a equação da reta tangente à elipse x 2 a 2 + y 2 b 2 = 1 no ponto x 0 ,y 0 da elipse é x 0 x a 2 +y 0 y b 2 = 1 .
Ache a equação da elipse tendo as propriedades dadas e faça um esboço do gráfico.Focos em ( 2 ,3 ) e ( 2 ,7 ) e o comprimento do semi-eixo menor é dois terços do comprimento do semi-eixo maior.
Na figura 11 prove que α = β . (Sugestão: escolha os eixos coordenados de tal forma que o centro da elipse esteja na origem e os eixos ao longo dos eixos coordenados. Então use o Teorema 1.6.8.)
A órbita da Terra em torno do Sol é uma elipse com o Sol em um foco e um semi–eixo maior com 149,5 milhões de quilômetros. Se a distância entre os focos for de 5,08 milhões de quilômetros, ache (a) a