Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.2 - Ex. 31

Na figura 11 prove que α = β . (Sugestão: escolha os eixos coordenados de tal forma que o centro da elipse esteja na origem e os eixos ao longo dos eixos coordenados. Então use o Teorema 1.6.8.)

Passo 1

Tomemos P como um ponto qualquer da elipse x 2 a 2 + y 2 b 2 = 1 e os ângulos α   e   β estão entre as distâncias focais e a reta PT tangente à elipse.

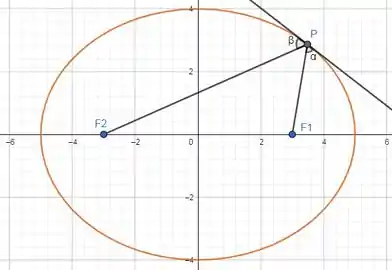
Passo 2

Vamos colocar os valores dos coeficiente angular das retas que cruzam para formar β e assim apliquemos o Teorema 1.6.8

tan ⁡ β = m 2 - m 1 1 + m 1 m 2

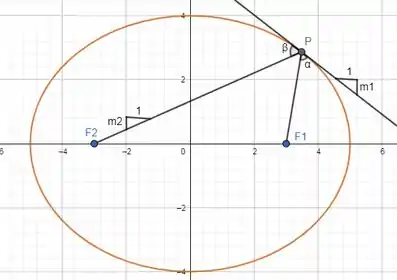
Passo 3

Agora devemos encontrar m 1 e m 2 . Para achar m 1 basta derivar a equação da elipse no ponto dado. Assim temos

d x 2 a 2 + y 2 b 2 d x   = d 1 d x  

2 x a 2 + 2 y y ' b 2 = 0

2 y y ' b 2 = - 2 x a 2

Agora vamos isolar y '

m 1 = y ' = - b 2 x a 2 y

Passo 4

Agora para achar m 2 vamos usar a seguinte fórmula Δ y Δ x . Para isso usaremos os dois pontos conhecidos nesta reta: F2 ( - c ,   0 ) e P ( x ,   y ) .

m 2 = Δ y Δ x = y x - - c =   y x + c

Aplicando os coeficientes encontrados teremos a seguinte equação

tan ⁡ β = y x + c - - b 2 x a 2 y 1 + y x + c - b 2 x a 2 y  

Vamos Aplicar o M.M.C e algumas manipulações nesta equação.

tan ⁡ β = a 2 y 2 + b 2 x x + c x + c a 2 y x + c a 2 y - b 2 x y x + c a 2 y

tan ⁡ β = a 2 y 2 + b 2 x x + c x + c a 2 y - b 2 x y

Agora aplicaremos distributiva

tan ⁡ β = a 2 y 2 + b 2 x 2 + b 2 x c a 2 y x + a 2 y c - b 2 x y

Agora colocaremos o termo em comum em evidência

tan ⁡ β = a 2 y 2 + b 2 x 2 + b 2 x c ( a 2 - b 2 ) y x + a 2 y c

Passo 5

Sabemos que nas elipses c 2 = a 2 - b 2 e x 2 a 2 + y 2 b 2 = 1   ⇒ a 2 y 2 + b 2 x 2 =   a 2 b 2   . Logo temos

tan ⁡ β = a 2 b 2 + b 2 x c c 2 y x + a 2 y c

tan ⁡ β = b 2 a 2 + x c c y x c + a 2

tan ⁡ β = b 2 c y

Agora farremos o mesmo para α

tan ⁡ α = m 1 - m 3 1 + m 1 m 2

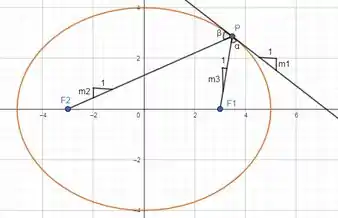
Passo 6

Agora para achar m 3 vamos usar a seguinte fórmula Δ y Δ x . Para isso usaremos os dois pontos conhecidos nesta reta: F2 ( c ,   0 ) e P ( x ,   y ) .

m 3 = Δ y Δ x =   y x - c

Assim temos

tan ⁡ α = - b 2 x a 2 y - y x - c 1 + - b 2 x a 2 y y x - c

Vamos Aplicar o M.M.C e algumas manipulações nesta equação.

tan ⁡ α = - b 2 x x - c - a 2 y 2 x - c a 2 y x - c a 2 y - b 2 x y x - c a 2 y

Agora aplicaremos distributiva

tan ⁡ α = - b 2 x x - c - a 2 y 2 x - c a 2 y - b 2 x y

tan ⁡ α = - b 2 x 2 + b 2 x c - a 2 y 2 a 2 y x - a 2 y c - b 2 x y

Aplicaremos as mesmas relações ditas anterioremente para tan ⁡ β

tan ⁡ α = - ( b 2 x 2 + a 2 y 2 ) + b 2 x c ( a 2 - b 2 ) x y - a 2 y c

tan ⁡ α = - a 2 b 2 + b 2 x c c 2 x y - a 2 y c

Agora colocaremos o termo em comum em evidência

tan ⁡ α = b 2 - a 2 + x c c y ( c x - a 2 )

tan ⁡ α = b 2 c y

tan ⁡ α = tan ⁡ β =   b 2 c y

Se tan ⁡ α = tan ⁡ β =   b 2 c y , então podemos dizer que α = β .

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o centro, vértices, focos, extremidade do eixo menor da elipse dada. Faça um esboço da curva, mostrando os focos. 16 x 2 + 4 y 2 = 1
Ache o centro, vértices, focos, extremidade do eixo menor da elipse dada. Faça um esboço da curva, mostrando os focos. 3 x 2 + 5 y 2 - 6 x - 12 = 0
Ache o centro, vértices, focos, extremidade do eixo menor da elipse dada. Faça um esboço da curva, mostrando os focos. 9 x 2 + 4 y 2 - 18 x + 16 y - 11 = 0
Ache o centro, vértices, focos, extremidade do eixo menor da elipse dada. Faça um esboço da curva, mostrando os focos. 5 x 2 + 3 y 2 - 3 y - 1 2 = 0
Determine se o gráfico da equação dada é uma elipse, um ponto ou um conjunto vazio. 2 x 2 + 3 y 2 + 8 x - 6 y + 20 = 0