Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 12
Calcule a área do quadrado de lados paralelos aos eixos coordenados, inscrito na elipse de equação .
Passo 1
Eita, pelo enunciado esta questão parece ser bem complicada!
E aí, o que precisamos fazer? Vamos começar fazendo um esboço da elipse e desenhar o nosso quadrado. Talvez isto ajude. Portanto,
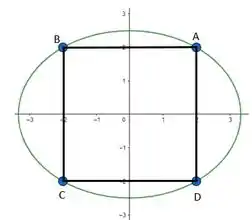
Este desenho é interessante para percebermos a simetria dos pontos em relação aos eixos coordenados. Se temos um vértice , notem que as coordenadas e são iguais pois estamos falando de um quadrado, temos os seguintes vértices então:
De forma que o lado do quadrado é , e, portanto, sua área será:
Portanto, nosso trabalho será encontrar este .
Passo 2
E agora, como encontraremos este ponto ?
Bom, nós já não sabemos que seu vértice tem coordenadas ? E também que este vértice pertence a elipse, e, portanto, satisfaz a sua equação?
Pronto! Esta é a sacada! Basta substituirmos as coordenadas do ponto na equação da elipse e assim descobrirmos o valor e ! Logo,
E assim chegamos ao valor de . Assumimos apenas o valor positivo, pois, como o ponto está no primeiro quadrante, então, . Continuando, a área do nosso quadrado será: