Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 28.Problemas - Ex. 10
Calcule o cosseno do ângulo formado por duas diagonais de um cubo.
Passo 1
Saudações galerinha, tudo bem?
Vamos começar a resolver mais um exercício, bora lá então!
Para esse exercício vamos utilizar a trigonometria básica. Inicialmente vamos desenha nosso cubo:
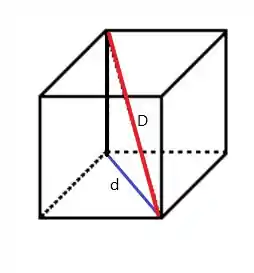
Observamos que nosso cubo possui duas faces a primeira é bem fácil pois se trada da diagonal da face representada por , como o ângulo será , o .
Agora vamos encontrar a diagonal , aplicando o teorema de Pitágoras!
Antes disso, tudo na tranquilidade?
Passo 2
Aplicando o teorema de Pitágoras, para o triângulo de altura e base descrito na imagem acima, teremos:
Último passo, quase acabando!
Passo 3
Vamos encontrar o cosseno, lembrando que
Substituindo vamos obter:
Simplificando:
Prontinho!
Acabamos te vejo na próxima questão!