Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 7.Exercícios Propostos - Ex. 5

  1. Calcule m de modo que as retas r e s sejam concorrentes:

    2.         ⎧   x   =   4   +   2 α

    r     ⎢   y   =   - 2 + m α e

            ⎩   z   =   4 + α

            ⎧   x   =   3   -   β

    s     ⎢     y   =   - 4 + 3 β

            ⎩   z   =   2 + β

  2. Escreva uma equação do plano determinado por r e s .
  3. Ache equações paramétricas da reta t que passa pela interseção de r e s e é perpendicular ao plano que r e s determinam.

Passo 1

  1. Retas concorrentes são retas que se encontram em um ponto. Nesse ponto, devemos ter

    2. 4   +   2 α =   3   -   β ⇒ β = - 1 - 2 α

    - 2 + m α = - 4 + 3 β ⇒ m α = 3 β - 2 = - 3 - 6 α - 2 = - 5 - 6 α ⇒ m = - 5 - 6 α α

    4 + α =   2 + β ⇒ β = α + 2

    Igualando os resultados da primeira e da segunda equação, obtemos

    - 1 - 2 α = α + 2 ⇒ 3 α = - 3 ⇒ α = - 1

    Agora , substituímos α = - 1 no resultado da segunda equação

    m = - 5 - 6 α α = - 5 + 6 - 1 = - 1

    Passo 2

  2. Para determinar o plano contendo as duas retas, temos que identificar dois vetores contidos no plano. Esses vetores são os vetores diretores das retas:

    3. v → r = ( 2 , m , 1 ) = ( 2 , - 1,1 )

    v → s = ( - 1,3 , 1 )

    Agora, precisamos de um terceiro vetor que seja l.d. com os dois vetores acima. Sabemos que o ponto R = ( 4 , - 2,4 ) pertence a reta r (quando α = 0 ). Supondo que temos um ponto P = ( x , y , z ) no plano, podemos definir o vetor

    P R → = R - P = ( 4 , - 2,4 ) - ( x , y , z ) = ( 4 - x , - 2 - y , 4 - z )

    Os vetores P R → , v → r e v → s devem ser l.d., então

    ⇒ ( 4 - x ) ( - 1 - 3 ) - ( - 2 - y ) ( 2 + 1 ) + ( 4 - z ) ( 6 - 1 ) = 0

    ⇒ - 4 ( 4 - x ) - 3 ( - 2 - y ) + 5 ( 4 - z ) = 0

    ⇒ - 16 + 4 x + 6 + 3 y - 5 z + 20 = 0

    ⇒ 4 x + 3 y - 5 z + 10 = 0

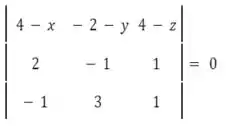
    Passo 3

  3. No item a), nós mostramos que as duas retas se encontram quando α = - 1 . Nesse caso, temos como ponto de interseção:

  x   =   4   +   2 α = 4 - 2 = 2

y = - 2 - α = - 2 + 1 = - 1

z   =   4 + α = 4 - 1 = 3

ou seja, P = ( 2 , - 1,3 ) . Se a reta t passa por esse ponto, então suas equações paramétricas são

x   =   2 +     u t

y = - 1 + v t

z   =   3 + w t

onde o vetor diretor será v → t = ( u , v , w ) . Como a reta t é perpendicular ao plano que r e s determinam, então devemos ter

v → t ⋅ v → s = 0 ⇒ ( u , v , w ) ⋅ ( - 1,3 , 1 ) = 0 ⇒ - u + 3 v + w = 0

v → t ⋅ v → r = 0 ⇒ ( u , v , w ) ⋅ ( 2 , - 1,1 ) = 0 ⇒ 2   u - v + w = 0

Vamos multiplicar a primeira equação por 2 e somar com a segunda:

6 v - v + 2   w + w = 0 ⇒ 5 v + 3 w = 0 ⇒ v = - 5 3 w

Agora, subtraindo a primeira equação da segunda:

2 u + u - 3 v - v = 0 ⇒ 3 u - 4 v = 0 ⇒ u = 4 3 v

A equação paramétrica vai ficar mais ou menos assim:

x   =   2 + 4 3 v t

y = - 1 + v t

z   =   3 - 5 3 v t

Não temos mais nenhuma restrição que nos permita determinar v . Então, podemos escolher v = 3 para o resultado ficar mais agradável:

x   =   2 + 4 t

y = - 1 + 3 t

z   =   3 - 5 t

Resposta

  1. m = - 1
  2. 4 x + 3 y - 5 z + 10 = 0
  3. x   =   2 + 4 t , y = - 1 + 3 t , z   =   3 - 5 t

Exercícios de Livros Relacionados

Escreva uma equação cartesiana do plano paralelo ao eixo O z e que passa pelos pontos A = ( 6,2 , - 1 ) e B = 3,4 , - 3 .
Dados o plano π : 2 x - y - 2 z - 3 = 0 e o ponto A = - 4,6 , 5 , pedem-se:(a)equações da reta r que passa por A e é perpendicular ao plano π ; (b) as coordenadas do ponto de interseção entre r e π ;(
Escreva uma equação cartesiana do plano determinado pelo ponto ( 1,2 , 1 ) e pela reta x - 1 2 = y - 1 - 1 = z
Calcule as coordenadas do ponto A ' , projeção ortogonal de A = 4,0 , 2 sobre o plano 3 x - y - z + 23 = 0
Dados os pontos A = 1,1 , 3eB = ( 1,3 , 1 ) , ache uma equação do plano ortogonal ao segmento A B e passando pelo seu ponto médio.