Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 24.Exercício - Ex. 35
Calcule para que o plano seja tangente a superfície esférica , e determine o ponto de tangência.
Passo 1
O centro dessa superfície esférica encontra-se na origem e o vetor normal encontra-se em , portanto o ponto de tangência será:
Aplicando esse ponto na esfera nós teremos:
Aplicando na equação do plano nós teremos
A figura dessa superfície com o plano pode ser visto abaixo.
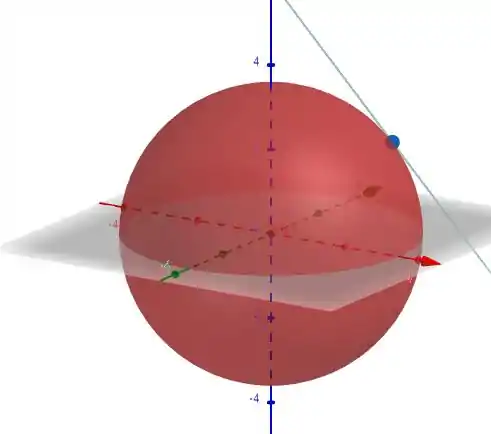
Passo 2
E aplicando na equação do plano nós teremos e a figura desse plano pode ser vista abaixo.
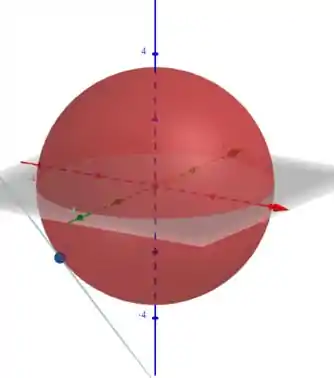
Essa questão tem uma quebra de normalidade, por que estávamos ficando acostumados em encontrar o raio da esfera com a equação do plano lá, nesse ele te dá a equação da esfera toda bonitinha, mas não necessariamente o plano o vetor irá ficar daquela forma, ela estará proporcional com o tamanho do raio e isso que temos que ficar ligados.
Resposta
Ou