Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Elipse - Ex. 17
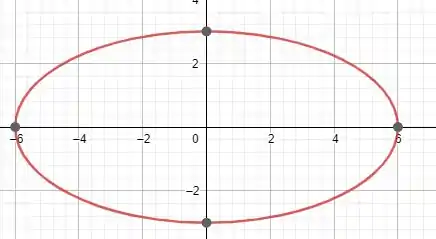
Centro , eixo menor igual a 6, focos no eixo dos e passando pelo ponto ;
Passo 1
O eixo menor vale 6, então:
Substituindo o ponto dado na equação:
Nossa equação será:
Passo 2
A equação dessa elipse será dada por:
Onde os termos marcados em e 3 marcado em .
Resposta
Exercícios de Livros Relacionados
Nos problemas 34 a 39, obter equações paramétricas da elipse de equação dada. x 2 + 4 y 2 = 4
Nos problemas 34 a 39, obter equações paramétricas da elipse de equação dada. x 2 + y 2 = 36
Em cada um dos problemas 28 a 33, determinar a equação reduzida, o centro, os vértices A 1 e A 2 , os focos e a excentricidade das elipses dadas. Esboçar o gráfico 16 x 2 + 9 y 2 - 96 x + 72 y + 14 4
Em cada um dos problemas 28 a 33, determinar a equação reduzida, o centro, os vértices A 1 e A 2 , os focos e a excentricidade das elipses dadas. Esboçar o gráfico 4 x 2 + 9 y 2 - 8 x - 36 y + 4 = 0
Um satélite de órbita elíptica e excentricidade 1 3 viaja ao redor de um planeta situado em um dos focos da elipse. Sabendo que a distância mais próxima do satélite ao planeta é de 300k m , calcular a