Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 129
Dê condições sobre e para que o losango cujos vértices são os focos e as extremidades do eixo conjugado da hipérbole seja um quadrado. Calcule a área do losango.
Passo 1
Um losango é a figura plana onde os quatro lados são congruentes, e as diagonais são perpendiculares.
Se as medidas das diagonais medem, respectivamente, e , então a área do losango será:
No caso da questão, podemos fazer a seguinte construção
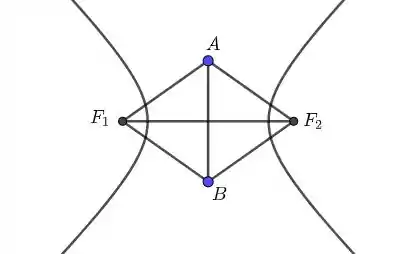
onde e são os focos e são as extremidades do eixo conjugado.
O losango será um quadrado quando suas diagonais forem congruentes.
Passo 2
Temos que
onde . Logo:
Passo 3
Para que as diagonais sejam congruentes:
o que é impossível. Logo, o losango em questão nunca pode ser um quadrado!
Resposta
O losango nunca poderá ser um quadrado. A área será .
Exercícios de Livros Relacionados
Ache a menor distância do ponto 2 ,- 5 à reta 3 x + y = 2 .
Ache uma equação da reta perpendicular à reta que passa pelos pontos - 1 ,5 e 3 ,2 no ponto médio desse segmento da reta.
Os lados de um paralelogramo estão sobre as retas x + 2 y = 10 , 3 x - y = - 20 , x + 2 y = 15 e 3 x - y = - 10 . Ache as equações das diagonais se determinar os vértices do paralelogramo. (Sugestão:
Ache uma equação da circunferência que circunscreve o triângulo cujos lados estão sobre as retas x - 3 y + 2 = 0 , 3 x - 2 y + 6 = 0 e 2 x + y - 3 = 0 .
Determine se a função é par, ímpar ou nem par e nem ímpar. g x = 5 x 4 + 2 x 2 - 1