Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 3.1 - Ex. 32
33 Considere a Figura 3.1.12. Discuta uma interpretação geométrica do vetor.
Passo 1
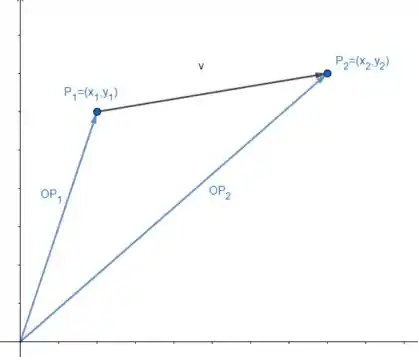
Vamos pensar em cada parte dessa equação para entender o vetor. Vamos chamar de , ou seja, é o vetor que liga os pontos e assim como na Figura 3.1.12.
Passo 2
Quando multiplicamos esse vetor por temos metade do vetor orginal, vamos chamar esse vetor de :
Ele fica assim:
Passo 3
E por fim devemos somar com :
Quando a gente somar esses dois vetores devemos juntar o pont inicial de com o ponto final de , dessa forma vamos obter:
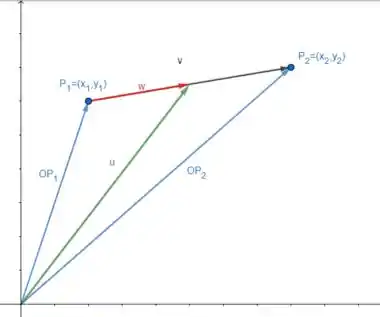
Ou seja, esse vetor mostar onde esta o ponto médio do segmento de reta que une os pontos com .
Resposta
Esse vetor mostar onde esta o ponto médio do segmento de reta que une os pontos com .
Exercícios de Livros Relacionados
Nos Exercícios 13-16, determine se os planos dados são paralelos - 4,1 , 2 ⋅ x , y , z = 0 8 , - 2 , - 4 ⋅ x , y , z = 0
Nos exercícios 21-28, encontre os componentes vetoriais de u → ao longo de e ortogonal a a → u = 6,2 a = ( 3 , - 9 )
Nos exercícios 19-20, encontre | p r o j a u → | u → = 5,6 ,a → = ( 2 , - 1 )
Nos exercícios 19-20, encontre | p r o j a u → | u → = 1 , - 2 ,a → = ( - 4 , - 3 )
Nos exercícios 19-20, encontre | p r o j a u → | u → = 3 , - 2,6 ,a → = ( 1,2 , - 7 )