Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 5.6 - Ex. 19

Considere a transformação linear:

T : R 3 → R 3 dada por T x , y , z = ( z , x - y , - z )

  1. Determine uma base do núcleo de T .
  2. Dê a dimensão da imagem de T .
  3. T é sobrejetora? Justifique.
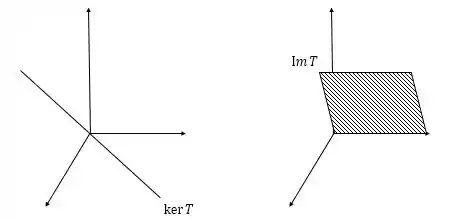
  4. Faça um esboço de ker ⁡ T e I m T .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Temos que:

ker ⁡ T = v ∈ V ;   T v = 0

Ou seja:

( z , x - y , - z ) = 0

Temos que:

z = 0

x - y = 0

x = y

Logo:

ker ⁡ T = x , x , 0 = x ( 1,1 , 0 )

ker ⁡ ( T ) = ( 1,1 , 0 )

Portanto ( 1,1 , 0 ) é base de ker ⁡ T .

Passo 2

Para a imagem temos:

I m   T : T v = w

T v = ( z , x - y , - z )

T v = x 0 , 1 , 0 + y 0 , - 1 , 0 + z ( 1,0 , - 1 )

Temos que 0,1 , 0 , 0 , - 1,0 , ( 1,0 , - 1 ) , são linearmente dependentes, portanto:

0,1 , 0 , ( 1,0 , - 1 ) é base de I m   ( T ) .

Logo:

dim ⁡ I m   ( T ) = 2

Passo 3

Para ser sobrejetora, a imagem deve ser igual ao contradomínio, ou seja:

dim ⁡ I m   ( T ) = dim ⁡ R 3

Como:

2 ≠ 3

Não é sobrejetora.

Passo 4

Temos que:

Resposta

a ) ( 1,1 , 0 )

b ) dim ⁡ I m   T = 2

c )   N ã o   é   s o b r e j e t o r a ,   p o i s   a   d i m e n s ã o   d a   i m a g e m   é   d i f e r e n t e   d a   d i m e n s ã o   d o   c o n t r a d o m í n i o .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja T : R 2 → R 2 uma reflexão, através da reta y = 3 x .Encontre T ( x , y ) .Encontre a base α de R 2 , tal que T α α = 1 00 - 1
Dados T : U → V linear e injetora e u 1 , u 2 , … ,u k , vetores L I em U mostre que T u 1 ,… ,T ( u k ) é L I .
No plano, uma rotação anti-horária de 45 ° é seguida por uma dilatação de 2 . Ache a aplicação A que representa esta transformação no plano.
Mostre que se T : V → W é uma transformação linear: I m ( T ) é subespaço de W . k e r ⁡ ( T ) é subespaço de V .
Ache a transformação T do plano no plano que é uma reflexão em torno da reta x = y .Escreva-a em forma matricial.