Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 3.1 - Ex. 17

Considere o triângulo ABC e sejam M o ponto médio de BC, N o ponto médio de AC e P o ponto médio de AB. Mostre que as medianas (os segmentos AM, BN e CP) se cortam num mesmo ponto que divide as medianas na proporção 2/3 e 1/3. (Sugestão: Sejam G, H e I os pontos definidos por A G → = 2 3 A M → , B H → = 2 3 B N → e C I → = 2 3 C P → . Mostre que G H → = 0 → , G I → = 0 → , conclua que G = H = I).

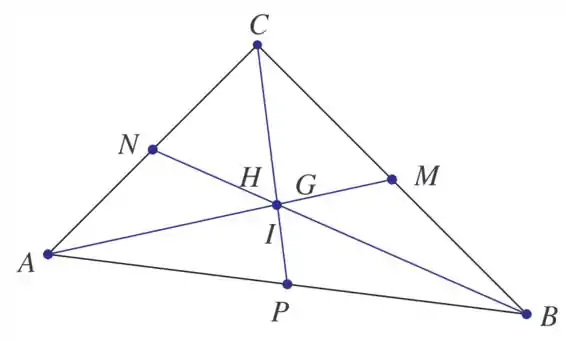
Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de geometria analítica.

Para responder ao questionamento do enunciado, usamos a seguinte equação vetorial:

G H → = H B → + B A → + A G →

Da figura temos que:

A G → = 2 3 A M → ;   H B → = - 2 3 B N →   e   B A → = B H → + G A →

Reescrevendo a equação vetorial temos que:

G H → = - 2 3 B N → + B H → + G A → + 2 3 A M → = - 2 3 B N → + 2 3 B N → - 2 3 A M → + 2 3 A M → = 0 →

Com isso demonstramos que G = H.

Passo 2

Seguindo o mesmo procedimento vamos demonstrar que G I → = 0 → .

usamos a seguinte equação vetorial:

G I → = I C → + C A → + A G →

Da figura temos que:

A G → = 2 3 A M → ;   I C → = - 2 3 C P →   e   C A → = C I → + G A →

Reescrevendo a equação vetorial temos que:

G I → = - 2 3 C P → + C I → + G A → + 2 3 A M → = - 2 3 C P → + 2 3 C P → - 2 3 A M → + 2 3 A M → = 0 →

Com isso demonstramos que G = I.

E por conseguinte temos que G = H = I.

Resposta

Ver passo a passo.

Exercícios de Livros Relacionados

Demonstre que, se V e W são vetores quaisquer, então: (a): V . W = 1 4 ( V + W 2 - V - W 2 )
Demonstre que se V e W são vetores quaisquer, então: (c): V - W ≤ V - W ;
Demonstre que se V e W são vetores quaisquer, então: (a): V . W ≤ V W ;
Sugestão para os próximos 2 exercícios: Considere o paralelogramo A B C D . Seja U =A B → e V =A D → . Observe que as diagonais do paralelogramo são U + V e U - V .
Sejam V um vetor não nulo no espaço e α , β e γ os ângulos que V forma com os vetores i → , j → , k → , respectivamente. Demonstre que cos 2 ⁡ α + cos 2 ⁡ β + cos 2 ⁡ γ = 1