Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 2ª Edição - Alfredo Steinbruch e Paulo Winterle- Ed: 2º - Capítulo 4.8 - Ex. 33
Consideremos o operador linear
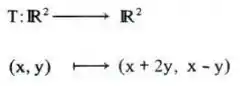
e as bases , e canônica. Determinar , e .
Passo 1
A questão forneceu uma transformação linear e pede para escrevermos a matriz de transformação em diferentes bases. Vamos fazer primeiro na base canônica:
Assim
Passo 2
Agora vamos tentar escrever . Para isso, vamos calcular a transformação sobre os vetores da base de :
Passando para a base :
Assim, vemos que e . Logo,
Analogamente,
Logo, e :
Desta forma, a matriz será
Passo 3
Por fim, vamos procurar :
Escrevendo na base :
Assim,
Resolvendo esse sistema, encontramos e . Assim,
Da mesma forma,
Assim,
Resolvendo o sistema, temos e . Assim,
Portanto, a matriz de transformação nessa base será
Resposta
Exercícios de Livros Relacionados
(Requer Cálculo) Projete um método de usar a multiplicação matricial para derivar funções do espaço vetorial g e r 1 , sin x , cos x , sin 2 x , cos 2 x . Use o método projetado para encontrar
Determinar um operador linear F :R 3 → R 3 cuja imagem é gerada por ( 2 ,1 ,1 ) e ( 1 ,-1 ,2 ) .
Determinar um operador linear do R 3 cujo núcleo tenha dimensão 1 .
Mostrar que cada um dos operadores lineares do R 3 a seguir é inversível e determinar o isomorfismo inverso em cada caso:(a )F ( x ,y ,z )=( x-3 y-2 z ,y-4 z ,z ) ; (b) F ( x ,y ,z )=( x ,x -y ,2 x+y-
Mostrar que cada um dos operadores lineares do R 3 a seguir é inversível e determinar o isomorfismo inverso em cada caso:(a )F ( x ,y ,z )=( x-3 y-2 z ,y-4 z ,z ) ; (b) F ( x ,y ,z )=( x ,x -y . ,2 x+