Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento algébrico - Ex. 26b
26. Construir o cubo constituído dos pontos , de modo que:
b)
Passo 1
Então galera, para construirmos esse cubo devemos encontrar os pontos que constituem os vértices desse cubo a partir dos intervalos dados pelo enunciado, mas como fazemos isso? É simples, galera, basta fazermos uma combinação entre os extremos de e . Os intervalos dados são:
Escrevendo de outra forma:
Fazendo a combinação entre esses intervalos obteremos os seguintes pontos, pessoal:
Show!
Passo 2
Note que da combinação que fizemos conseguimos extrair exatos pontos, que condiz com a quantidade de vértices de um cubo! Colocando esses pontos em um sistema de coordenadas tridimensional, teremos algo assim:
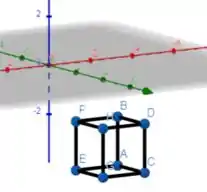
Vale ressaltar que como a figura é é importante ter uma noção de perspectiva para entender melhor a geometria da figura, ok? E esse é o nosso cubo, guys! 😉
Resposta
