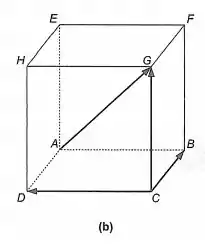
(e) O cubo da Figura 11-7(b) tem aresta unitária e está submetido às forças aplicadas indicadas. Determine a força adicional que deverá ser exercida sobre ele para que haja equilíbrio e em que ponto ela deve ser aplicada.

Inicialmente, devemos somar as forças que partem do vértice , o que resultará em uma resultante saindo do vértice e chegando no vértice .

Agora, vamos somar a resultante com a força restante, usaremos o nosso conhecido teorema dos cossenos para calcular a norma do vetor resultante:

Como vamos somar forças que estão em um plano de simetria passando pelo centro do cubo, a aplicação da força para deixar o cubo em equilíbrio deve estar no eixo que é a interseção dos planos de simetria verticais do cubo.

Logo, para que o que foi dito no passo 4 seja possível, a força deve passar pelo encontro dos eixos de simentria verticais do cubo, e possuir normal igual a , sendo a norma das forças que acompanham as arestas do cubo, na figura.