Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 18.Exercício - Ex. 45

Um cubo tem diagonal A B e uma das faces está contida no plano π : x - y = 0 . Sabendo que A = 1,1 , 0 e B = 1,3 , 2 , determine os demais vértices (SO).

Passo 1

Considere a seguinte figura ( O não representa a origem na figura abaixo, é apenas um ponto)

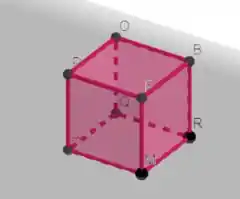
Note que A ∈ π . Suponha ainda que A P O Q seja o plano π . Vamos começar calculando as coordenadas de P :

Passo 2

Como P ∈ π , então x P = y P . Assim, P = x P ,   x P ,   z P .

d A ,   B = 1 - 1 2 + 1 - 3 2 + 0 - 2 2 = 6

Como A B é uma diagonal do cubo, então d A , B = 3 l , sendo l o lado do cubo. Assim,

3 l = 6 ⟹ l = 2

Então conseguimos encontrar mais duas equações para P :

d P ,   A = 2 d P ,   B = 2

pois P B é a diagonal de um quadrado de lado 2 .

Passo 3

Elevando ao quadrado e desenvolvendo:

x P - 1 2 + x P - 1 2 + z P 2 = 2 x P - 1 2 + x P - 3 2 + z P - 2 2 = 4 ⟹ 2 x P 2 + z P 2 - 4 x P = 0 2 x P 2 + z P 2 - 8 x P - 2 2 z P + 8 = 0

Subtraindo as equações, ficamos com

4 x P + 2 2 z P = 8 ⟹ 2 x P + 2 z P = 4 ∴ z P = 4 - 2 x P 2 = 2 2 - x P

Assim, colocando na primeira equação:

2 x P 2 + 2 4 - 4 x P + x P 2 - 4 x P = 0 ⟹ 4 x P 2 - 12 x P + 8 = 0 ∴ x P 2 - 3 x P + 2 = 0

x P - 1 x P - 2 = 0

Logo, teremos duas opções: x P = 1 e x P = 2 . Logo, z P = 2 ou z P = 0 .

Passo 4

A pergunta que surge é: por qual motivo encontramos duas coordenadas possíveis para P ? Note que tanto P quanto Q estão no plano π , e são equidistantes de A e B ! Logo, na verdade achamos as coordenadas de P e Q !! Assim, para fixar, considere P = 1,1 , 2 e Q = 2,2 , 0 .

Passo 5

Note que podemos encontrar os pontos restantes apenas por equipolência de vetores. Note que:

P A → = B R → ⟹ A - P = R - B ∴ R = A + B - P

R = 1,1 , 0 + 1,3 , 2 - 1,1 , 2 = 1,3 , 0

Também temos que

Q A → = R M → ⟹ A - Q = M - R ∴ M = A + R - Q

M = 1,1 , 0 + 1,3 , 0 - 2,2 , 0 = 0,2 , 0

Para determinar O :

B O → = R Q → ⟹ O = B + Q - R

O = 1,3 , 2 + 2,2 , 0 - 1,3 , 0 = 2,2 , 2

Por fim, para determinar F :

M F → = A P → ⟹ F = P + M - A

F = 1,1 , 2 + 0,2 , 0 - 1,1 , 0 = 0,2 , 2

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Problemas 25 a 30 , obter uma equação geral do plano:27) Paralelo ao eixo y e que contenha os pontos A ( 2 ,3 ,0 ) e B ( 0 ,4 ,1 ) .
Nos Problemas 23 e 24 , determinar uma equação geral do plano que contenha o ponto e a reta dados:23) A 4,3 , 2 r :x = t y = 2 - t 3 + 2 t
Nos Problemas 25 a 30 , obter uma equação geral do plano:26) Paralelo ao eixo x e que contenha os pontos A ( - 2 ,0 ,2 ) e B ( 0 ,- 2 ,1 ) .
Nos Problemas 25 a 30 , obter uma equação geral do plano:29) Perpendicular ao eixo y e que contenha o ponto A ( 3 ,4 ,- 1 ) .
Nos Problemas 23 e 24 , determinar uma equação geral do plano que contenha o ponto e a reta dados:23) A 1 , - 1,2 r :e i x oz