Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 1.1 - Ex. 15

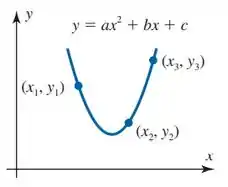
A curva y = a x 2 + b x + c mostrada na figura passa pelos pontos x 1 , y 1 ,   x 2 , y 2 e x 3 , y 3 . Mostre que os coeficientes a ,   b e c são uma solução do sistema de equações lineares cuja matriz aumentada é:

x 1 2 x 2 2 x 3 2 x 1 x 2 x 3 1 1 1 y 1 y 2 y 3

Passo 1

O sistema a x 1 2 + b x 1 + c = y 1 a x 2 2 + b x 2 + c = y 2 a x 3 2 + b x 3 + c = y 3 tem os pontos   x 1 , y 1 ,   x 2 , y 2 e x 3 , y 3 sendo as soluções

da equação y = a x 2 + b x + c

Passo 2

Se transformarmos esse sistema numa equação matricial, teremos:

x 1 2 x 2 2 x 3 2 x 1 x 2 x 3 1 1 1 a b c = y 1 y 2 y 3

Passo 3

Ignorando a matriz coluna a b c , teremos que     x 1 2 x 2 2 x 3 2 x 1 x 2 x 3 1 1 1 = y 1 y 2 y 3 .

Essa equação pode ser sintetizada numa matriz aumentada   x 1 2 x 2 2 x 3 2 x 1 x 2 x 3 1 1 1 y 1 y 2 y 3

Resposta

Portanto, a matriz aumentada que procuramos é   x 1 2 x 2 2 x 3 2 x 1 x 2 x 3 1 1 1 y 1 y 2 y 3 como queríamos provar.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considerando os 4 vetores-coluna u = (a1, a2), v = (b1, b2), w = (c1, c2) e d = (d1, d2), escreva o sistema de duas equações com três incógnitas sob a forma x·u+y·v+z·w = d e, a partir daí, interprete
. No sistema a 1 x+b 1 y+c 1 z=d 1 a 2 x+b 2 y+c 2 z=d 2, admitindo que se têm realmente três incógnitas, mostre que se a1b2 − a2b1 = b1c2 − b2c1 = c1d2 − c2d1 = 0 então existe k ≠ 0 tal que a2 = ka1,
Para cada um dos sistemas a seguir, decida se existem ou não soluções. No caso afirmativo, exiba todas as soluções do sistema em termos de um ou dois parâmetros independentes.x+2 y+3 z = 4 2 x-y+5 z=
Prove: se os vetores-coluna de uma matriz 3 × 3 são linearmente independentes então os vetores-linha da mesma matriz também são linearmente independentes
No sistema abaixo, atribua sucessivamente valores aos parâmetros m, n de modo que as três equações representem um único plano, dois planos ou três planos: x-2 y-3 z=m3 x-6 y-9 z=n- 2 x+4 y+6 z=1