Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 3.10 - Ex. 4

Dadas as matrizes

A = [[[1,2],[1,0]]] e B = [[[3,-,1],[0,1]]]

Calcule

  1. det A + det B ;
  2. det ( A + B ) .

Passo 1

Fala meu querido! Temos na nossa frente uma questão de calcular determinantes e operar algebricamente com matrizes 2 xx 2 . Para calcular esses determinantes dessas matrizes 2 xx 2 , vamos multiplicar os números da diagonal principal e subtrair o resultado pelo resultado da multiplicação dos números da diagonal secundária. Esse processo é chamado de Regra de Sarrus.

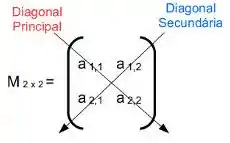
Passo 2

Para a matriz A :

det A = |[[1,2],[1,0]]| = 0 - 2 = - 2

Para a B :

det B = |[[3,-,1],[0,1]]| = 3 - 0 = 3

Então calculamos os determinantes das matrizes A e B e podemos fazer:

det A + det B = - 2 + 3 = 1

Passo 3

Para a letra b , ele não quer a soma dos determinantes como fizemos na letra a , ele quer o determinante da soma das matrizes A e B .

Então primeiro vamos somar as matrizes A e B :

A + B = [[[1,2],[1,0]]] + [[[3,-,1],[0,1]]] = [[[4,1],[1,1]]]

Vamos chamar essa nova matriz de C , então temos que:

A + B = C = [[[4,1],[1,1]]]

Logo:

det (A + B) = det (C) = |[[4,1],[1,1]]|

Para calcular esse determinante, vamos novamente usar o mesmo método de multiplicar e subtrair as diagonais:

det (C) = |[[4,1],[1,1]]| = 4 - 1 = 3

Então det (A + B) = 3

Resposta

  1. 1
  2. 3
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se A ou B é uma matriz não inversível, então A ∙ B também não é. Prove isto, sem usar determinantes.
Encontre A - 1 , onde 4 - 1 2 - 2 3 - 1 0 0 2 3 1 0 0 7 1 1 0 - i - 2 i 1 - 1 i 1 0 - 1 1 - i 1 1 1 0 1 0 x 1 1 x 2 2 2 x 2
Nos exercícios 1-4, verifique que det(kA)=k^n*det(A).
39. Mostre que se A for uma matriz quadrada, então det(A^TA)=det(AA^T)
38. Prove que uma matriz quadrada A é invertível se, e só se, A^TA é invertivel