Exercícios de Propriedades dos Determinantes - Lista de Exercícios Resolvida

As afirmativas abaixo tratam da matriz quadrada e da identidade . Qual das afirmativas é verdadeira?

Se a matriz é inversível, então

Se , então

Se é a matriz identidade de ordem , então

Se é , então

Seja uma matriz . Assinale a alternativa FALSA:

Se as linhas da matriz são linearmente dependentes, então

Diga se as alternativas abaixo são verdadeiras ou falsas:

1. Se e então
2. Se e então

Ambas são verdadeiras

I é verdadeira e II é falsa

I é falsa e II é verdadeira

Ambas são falsas

Calcule o determinante de , se

Encontre os valores de para os quais .

Seja uma matriz . Assinale a alternativa FALSA:

Se as linhas da matriz são linearmente dependentes, então

Para cada real, considere a transformação dada por:

Para quais valores de a transformação é inversível?

a) A soma de duas matrizes inversíveis é uma matriz inversível.

Considere as afirmativas abaixo:

1. Se é invertível então
2. Se e são matrizes quadradas e é invertível, então .

1. Ambas são verdadeiras
2. Ambas são falsas
3. I é falsa II é verdadeira
4. I é verdadeira e II é falsa

Qual é a condição sobre o valor que pode assumir para que a matriz seja inversível?

Considere a matriz

Calcule e, apartir deste, obtenha .

Obtenha, se possível, e .

Considere a matriz

Calcule o determinante da matriz .

Essa matriz é inversível? Se sim, calcule , se não, justifique.

Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmativa for falsa, exiba explicitamente um contraexemplo.

c) Se , então é invertível seja qual for .

d) Se , então tem nutilidade 2 seja qual for

Seja A uma matriz . Considere as afirmativas:

(I) Se , então

(II)

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Sejam e duas matrizes, respectivamente, e . Pode-se afirmar que:

(a)

(b)

(c)

(d)

Seja uma matriz quadrada com determinante nulo:

1. é injetiva.
2. é sobrejetiva.

I e II são verdadeiras.

I é verdadeira, mas II é falsa.

I é falsa, mas II é verdadeira.

I e II são falsas.

Considere a matriz dada por

Calcule o determinante de .

Sejam e matrizes quadradas de mesma ordem. Sabendo-se que

Podemos garantir que:

e

e

e

e

Quais são todos os valores de para os quais o operador linear dado por NÃO é invertível?

qualquer

Considere a matriz .

Calcule .

A matriz é inversível? Se sim, encontre sua inversa.

Quais são as operações elementares sobre as linhas de uma amtriz que não alteram o valor de seu determinante?

Calcule o determinante da matriz .

Essa matriz é inversível? Justifique.

Use a definição de determinante para calcular

Use a definição de determinante para calcular

Considere a matriz:

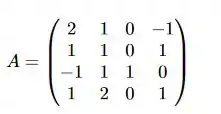
E denote a sua transposta. Temos que é igual a:

1. -26
2. 55
3. 0
4. 26
5. 81

Seja um inteiro positivo e sejam A e B matrizes reais Considere as seguintes afirmações:

1. Se a transposta da matriz A é igual a -A, então

Assinale a alternativa correta

1. Todas as afirmações são necessariamente verdadeiras;
2. Apenas a afirmação III é necessariamente verdadeira;
3. Apenas a afirmação I é necessariamente verdadeira;
4. Apenas as afirmações I e III são necessariamente verdadeiras;
5. Apenas as afirmações I e II são necessariamente verdadeiras.

Sejam um inteiro positivo, A uma matriz real e Y uma matriz real Considere o sistema linear em que a matriuz de incógnitas reais é Pode-se afirmar que:

1. Se o sistema possui solução, então
2. Se o sistema não possui solução, então
3. Se o sistema possui solução, então
4. Se o sistema possui solução
5. Se então o sistema possui infinitas soluções .

Considere as afirmativas:

1. Seja uma matriz com ímpar. Se , então
2. Sejam e matrizes . Se não é injetiva então

A afirmativa é verdadeira e a afirmativa é verdadeira

A afirmativa é falsa e a afirmativa é verdadeira

A afirmativa é verdadeira e a afirmativa é falsa

A afirmativa é falsa e a afirmativa é falsa

Responda:

Seja operador linear, com e sejam e bases de , tais que . é inversível? Se sim, determine uma matriz para

Qual dos argumentos abaixo é aceitável?

Se é autovalor de , então é autovalor de , pois

, pois

Suponha que é autovalor de e é um autovetor associado. Então, como , podemos concluir que

Se e são soluções de , então é solução de , pois .

Sejam e matrizes quadradas de ordem . Considere as seguintes afirmações:

Se , onde as linhas de são permutações das linhas de , então

Qual das opções abaixo é CORRETA?

A afirmativa é falsa e é falsa.

A afirmativa é verdadeira e é falsa.

A afirmativa é falsa e é verdadeira.

A afirmativa é verdadeira e é verdadeira.

Seja uma matriz quadrada e considere o sistema linear . Classifique em Verdadeira ou Falsa as afirmativas abaixo:

Se o sistema tem solução, então é diferente de 0.

Se o sistema não tem solução, então é igual a 0.

(a) é verdadeira e é falsa

(b) é falsa e é verdadeira

(c) Ambas são verdadeiras

(d)Ambas são falsas

Verdadeiro ou Falso? Forneça uma justificativa para sua resposta.

Seja uma projeção sobre a reta . Sejam a matriz de numa base de e uma matriz invertível. Então,

Considere uma matriz ortogonal , ; isto é, uma matriz onde o conjunto de suas solunas é ORTONORMAL. Assinale abaixo um valor possível para

Considere as matrizes , e , onde , é a i-ésima coluna de , e ambas com determinantes positivos:

1. é negativo
2. é negativo

1. I é verdadeira e II é falsa
2. Ambas são falsas
3. Ambas são verdadeiras
4. I é falsa e II é verdadeira

Seja uma matriz quadrada com . Assinale a alternativa FALSA:

não é injetiva

As linhas de são linearmente dependentes.

O núcleo de tem dimensão maior que zero

é sobrejetiva

Sejam A e B matrizes quadradas Considere as afirmações abaixo:

(I) Se A e B são invertíveis, então AB é invertível.

(II) Se AB é invertível, então A e B são invertíveis.

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Sejam um inteiro maior ou igual a e uma matriz real . Considere as seguintes afirmações:

1. Se o determinante de é nulo, então existe uma linha de que é igual ao produto de alguma outra linha de por um número real

2. Se existe uma matriz real não nula tal que , então tem o determinante nulo

3. Se existe uma matriz real não nula tal que o produto não é inversível, então tem determinante nulo

a) Apenas 1 e 2 são verdadeiras

b) Apenas 1 e 3 são verdadeiras

c) Apenas 1 é verdadeira

d) Apenas 2 e 3 são verdadeiras

e) Apenas 2 é verdadeira

f) 1, 2 e 3 são verdadeiras

g) 1, 2 e 3 são falsas

h) Apenas 3 é verdadeira

Considere o sistema linear , onde é uma matriz e . Sem conhecer e , mas apenas a forma escalonada da matriz aumentada do sistema,

Nós não podemos afirmar que:

A terceira entrada de qualquer solução de é

admite infinitas soluções

admite solução

Seja tal que , Calcule

1. .
2. .
3. .
4. .

Considere a matriz

e) Determine, se possível, . Caso contrário, justifique.

Seja A uma matriz quadrada e considere o sistema Ax=b.

I – Se ele tem solução, então

II – Se ele não tem solução, então

(a) I é falsa e II é verdadeira.

(b) I é verdadeira e II é falsa.

(c) Ambas são falsas.

(d) Ambas são verdadeiras.

Diga se as afirmativas abaixo são verdadeiras ou falsas.

1. Se é invertível então
2. Se e são matrizes quadradas e é invertível, então é invertível.

é verdadeira e é falsa

Ambas são verdadeiras

é falsa e é verdadeira

Ambas são falsas

Identifique se cada afirmação é verdadeira ou falsa. Justifique.

1. Se uma matriz quadrada tem então a nulidade de
2. Seja . Se , então não é inversível.

Compute o determinante da matriz :

É dado que . Podemos afirmar que: