Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 6.Problemas propostos - Ex. 49d
Dado o ponto e o plano , determinar:
A distância de ao plano .
Passo 1
A distância do ponto ao plano é o módulo do vetor , ou seja, o seu comprimento, como dá pra ver na figura abaixo:
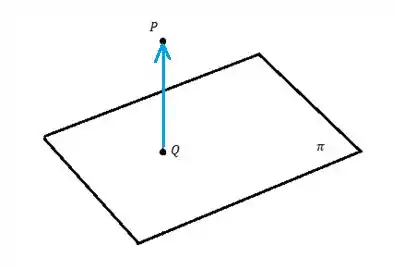
Primeiro vamos então encontra o vetor :
Passo 2
Pronto, agora vamos calcular o módulo do vetor, para calcular o módulo de um vetor vamos usar a fórmula tirada pelo Teorema de Pitágoras:
Pronto, vamos então aplicar essa fórmula para calcular o módulo:
Temos então que a distância de ao plano é de .
Resposta
Exercícios de Livros Relacionados
Obtenha, em cada caso, uma equação geral do plano π que contém r : X = 1 ,0 ,1 + λ ( 1 ,1 ,- 1 ) e dista d de P = ( 1 ,1 ,- 1 ) . Interprete os resultados de (a) e (b) usando o exercício resolvido ant
Obtenha uma equação geral do plano que contém os pontos A = ( 1 ,1 ,1 ) e B = ( 0 ,2 ,1 ) e equidista dos pontos C = ( 2 ,3 ,0 ) e D = ( 0 ,1 ,2 ) .
Mostre que os pontos A = - 2,0 , 1 , B = 0,0 , - 1 , C = 1,1 , 1 , D = - 2 , - 1 , - 2 e E = 1,2 , 2 são vértices de uma pirâmide e calcule seu volume.
Descreva o lugar geométrico dos pontos E 3 que eqüidistam dos planos π 1 : x + y - z = 0 , π 2 : x - y - z - 2 = 0 e π 3 : x + y + z = 1 .
Obtenha uma equação geral do plano que dista 1 de O = 0,0 , 0 e contém a reta perpendicular comum às retas r : X = 2,12 + λ 1,1 , 1 e s : X = - 1,0 , 1 + μ 1,1 , 2 .