Mostre que os pontos , , , e são vértices de uma pirâmide e calcule seu volume.
Passo 1
Tudo o que precisamos fazer aqui é: encontrar quatro pontos que formem um quadriáletro convexo plano. E depois mostrar que o quinto ponto não pertence a esse plano.
Se fizermos isso, então provamos que dá pra construir uma pirâmide com esses pontos!
Ok, então vamos começar procurando quatro pontos que sejam coplanares. Se os pontos , , e são coplanares, então:
E se esse conjunto é , então esse determinantes aqui é nulo:
Vamos testar isso para os pontos que o enunciado deu:
Substituindo isso na matriz e calculando o determinante:
Então os vetores são coplanares!
Passo 2
Beleza, então agora vamos encontrar a equação do plano formado por esses três vetores.
Pra isso primeiro precisamos definir um ponto qualquer , e então calcular esse produto misto:
Onde os pontos foram calculados assim!
Perceba que nem precisamos usar o ponto na conta! Já provamos que ele também pertence ao plano que passa por , e .
Agora vamos resolver aquele determinante:
E agora é só provar que o ponto não percente a esse plano. O ponto é:
Substituindo as coordenadas na equação do nosso plano:
O resultado não foi zero, e portanto não está no plano.
Passo 3
Ok, então até aqui já provamos que , , e pertencem a um plano em que não está!
Para garantir que isso forma uma pirâmide, ainda faltaria provar que os vetores entre , , e não são paralelos! Mas isso vai aparecer naturalmente quando a gente for calcular o volume.
Vamos fazer um desenho muito simplificado da nossa pirâmide:
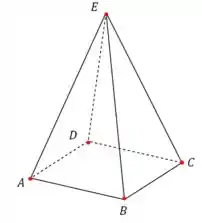
Antes de calcular o volume, precisamos descobrir se a base realmente tem essa forma no desenho, ou se a ordem dos pontos é diferente.
Pra isso vamos calcular a distância do ponto até os outros três:
O ponto mais distante de é , então podemos supor que e formam uma diagonal!
Com essa nova informação, vamos refazer nosso desenho:
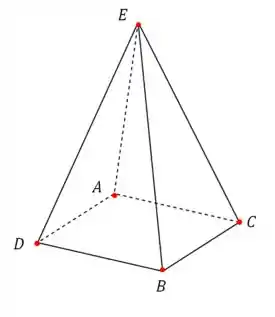
Passo 4
Agora como a gente pode calcular o volume dessa pirâmide? É só dividir em dois tetraedros!
O primeiro tetraedro é formado pelos vetores , e :
Vamos desenhar para entender melhor. Agora estamos calculando o volume da metade esquerda:
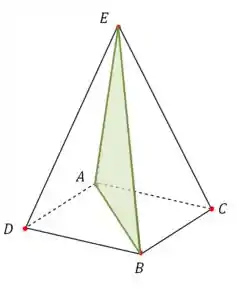
Agora é só usar a fórmula do volume do tetraedro:
E a outra metade é formada pelos seguintes vetores:
Então:
Somando essas duas partes:
Ou seja, os pontos formam uma pirâmide de volume igual a .
Resposta
Os pontos formam uma pirâmide de volume .