Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 6.Problemas propostos - Ex. 49c
Dado o ponto e o plano , determinar:
O ponto simétrico de em relação a .
Passo 1
Para encontrar o ponto simétrico de vamos visualizar eles na figura abaixo, para ficar mais claro:
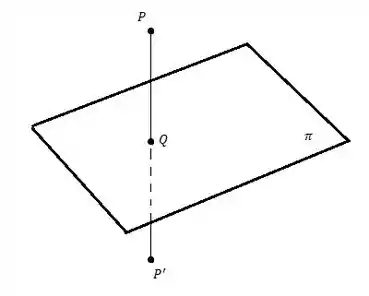
Hum, podemos analisar dois vetores aí, um que liga o ponto ao ponto e o outro que liga o ponto ao ponto , vamos ver eles dois na figura abaixo:
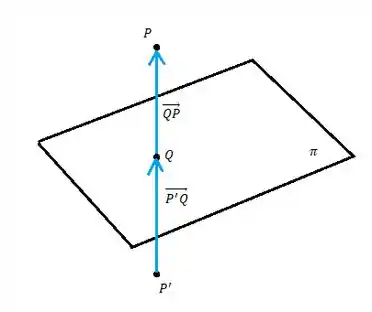
Pronto, dá pra perceber que os vetores e são iguais, vamos então igualar os dois para achar uma expressão para encontra :
Passo 2
Agora é só achar o vetor e conseguimos encontrar o ponto , vamos lá:
Vamos então substituir:
Pronto, temos que o ponto simétrico de em relação a é .
Resposta
Exercícios de Livros Relacionados
Uma pequena fábrica produz copos comuns e copos de vinho. Uma máquina automatiza parte do processo de fabricação. Para produzir uma caixa de copos comuns requer-se 1 hora de uso da máquina mais 1 hora
No exercício anterior, o que ocorre se o objetivo for maximizar x + 2y sujeito às mesmas restrições?
Um banco europeu dispõe de 100 milhões de euros para aplicar imediatamente.Duas opções lhe são oferecidas:Opção A: 10% ao ano, baixa liquidez.Opção B: 5% ao ano, alta liquidez.A diretoria decide que,
Para cada uma das regiões do plano descritas a seguir, escreva uma desigualdade ou sistema de desigualdades que a defina:b) A região formada pelo interior e os lados do triângulo cujos vértices são (0
Determine o menor valor que x + 2y assume no conjunto definido pelas desigualdades x + y ≥ 1 - x + y ≥ - 1 x ≥ 0 ,y ≥ 0