Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 21b
Dado o triângulo ABC não retângulo, e .
- Sendo AY a altura relativa ao vértice A e BZ a altura relativa ao vértice B, exprima em função de e em função de
Passo 1
Nesta letra b nós vamos ter algo mais ou menos assim:
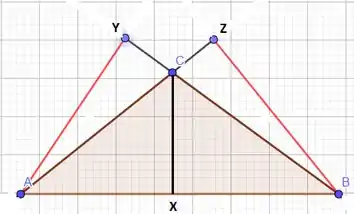
Segundo o enunciado nós teremos:
Agora se nós analisarmos o triângulo maior AYB:
Então:
Podemos reescrever como
Como
Pela soma vetorial:
Substituindo
Passo 2
Analogamente ao que vimos anteriormente:
Pela soma vetorial:
Substituindo
E finalizamos mais umaa !!
Resposta
Exercícios de Livros Relacionados
Quais são as projeções do ponto ( 2,3 , 5 ) nos planos x y , y z e x z ? Desenhe uma caixa retangular que tenha vértices opostos na origem e em ( 2,3 , 5 ) e suas faces paralelas aos planos coordenado
Determine uma equação da esfera com centro em ( 0 , 1 , - 1 ) e raio 4 . Qual é a intersecção dessa esfera com o plano y z ?
Determine se os pontos estão em uma mesma reta. A 2 , 4 , 2 ,B 3,7 , - 2 ,C ( 1,3 , 3 ) D 0 , - 5,5 ,E 1 , - 2,4 ,F ( 3,4 , 2 )
Encontre os comprimentos dos lados do triângulo P Q R . Ele é um triângulo retângulo? É isósceles?8. P 2 , - 1,0 ,Q 4,1 , 1 ,R ( 4 , - 5,4 )
Encontre os comprimentos dos lados do triângulo P Q R . Ele é um triângulo retângulo? É isósceles?7. P 3 , - 2 , - 3 ,Q 7,0 , 1 ,R ( 1,2 , 1 )