Dado o triângulo ABC, seja X a interseção do lado AB com a bissetriz do ângulo interno de vértice C (Figura 5-8) e sejam e .
- Explique geometricamente por que é paralelo a
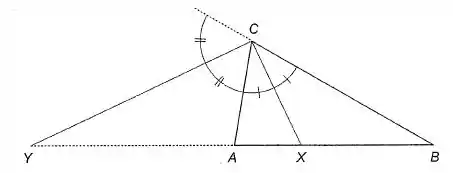
Passo 1
Bom galerinha, nós vamos começar deixando esse desenho mais bonito né?!
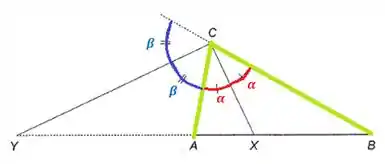
Pelo enunciado do problema nós temos que:
Então:
Sendo e versores, pela regra do paralelogramo sua soma será:
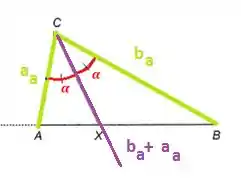
Então teremos que ou melhor:
Sabendo que, e :
Gostaram ?!