Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 18c
Dado o triângulo ABC, seja X a interseção do lado AB com a bissetriz do ângulo interno de vértice C (Figura 5-8) e sejam e .
- Mostre que X divide (A, B) na razão e conclua que
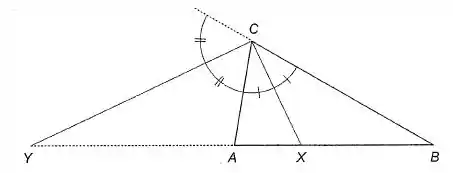
Passo 1
Vamos começar melhorando isso aqui, ok?
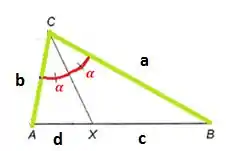
Então:
Como X divide AB na razão:
Por isso:
Ou melhor:
E fiiim !!
Resposta
Exercícios de Livros Relacionados
No triângulo ABC, P, Q e R são os pontos médios, respectivamente, de AB, BC, e AC. O ponto O é um ponto qualquer do espaço. Demonstre: O A→ +O B→ +O C →=O P →+O Q→ +O R →. (Sugestão: escreva O P → , O
Prove que o segmento que une os pontos médios de dois lados de um triângulo é paralelo ao terceiro lado e tem comprimento igual à metade do comprimento desse lado.
Seja ABC um triângulo qualquer com medianas A D ̄ , B E ̄ e C F ̄ . Demonstre que A D→ +B E→ +C F →=0 → .
No paralelogramo ABCD ao lado, temos D E → = αD C → , 3 B F → = F C → e G é a interseção das retas A E ̄ e D F ̄ . Determine α para termos A G → = 4 G E → ;a seguir, expresse w → = C G → como combinaç
Sejam A, B, C e D quatro pontos e M e N os pontos médios dos segmentos AC e BD. Determine, em função de M N → , a soma s → = A B →+A D→ +C B →+C D → .(Sugestão: A B →=A M→ +M N →+N B → e, analogamente