Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 16b
Sejam A, B e C vértices de um triângulo.
- Relacione o caso particular em que com o Exercício 5.4.
Passo 1
Vamos seguir pra letra (b)?
Nós já vimos que a situação descrita acima é representada pelo desenho:
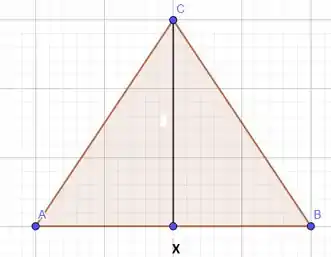
E da letra (a) nós vimos que:
Se:
Então:
De acordo com o Exercício 4(b), X pertence a AB se, e somente se, existem
Então, como e assumindo que concluímos que X pertence ao segmento AB!!
Tranquilinha, não foi?
Resposta
Exercícios de Livros Relacionados
Considere o triângulo ABC e sejam M o ponto médio de BC, N o ponto médio de AC e P o ponto médio de AB. Mostre que as medianas (os segmentos AM, BN e CP) se cortam num mesmo ponto que divide as median
Dados os pontos A = (1, −2, −3), B = (−5, 2, −1) e C = (4, 0, −1). Determine o ponto D tal que A, B, C e D sejam vértices consecutivos de um paralelogramo.
Verifique se é um paralelogramo o quadrilátero de vértices (não necessariamente consecutivos):A = (4, −1, 1), B = (9, −4, 2), C = (4, 3, 4) e D = (4, −21, −14)A = (4, −1, 1), B = (9, −4, 2), C = (4, 3
Demonstre que as diagonais de um paralelogramo se cortam ao meio. (Sugestão: Sejam M e N os pontos médios das duas diagonais do paralelogramo. Mostre que o vetor M N → = 0 → , então conclua que M = N)
Quais são as coordenadas do ponto P’, simétrico do ponto P = (1, 0, 3) em relação ao ponto M = (1, 2, −1)? (Sugestão: O ponto P’ é tal que o vetor M P ' → = - M P → ).