Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 19d
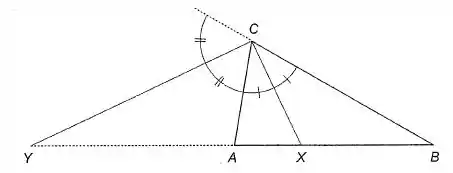
Dado o triângulo da Figura 5-8, sejam e suponhamos que . Seja Y a intersecção da reta AB com a bissetriz do ângulo externo do vértice C.
d) O que ocorreria se e fossem iguais?
Passo 1
Bom galerinha, se então:
Da questão anterior nós temos que:
Ou melhor:
Então para que Y existisse o ponto B deveria ser igual ao ponto A, o que seria impossível !!
Resposta
Exercícios de Livros Relacionados
Quais dos seguintes vetores são paralelos U = (6, −4, −2), V = (−9, 6, 3), W = (15, −10, 5).
Verifique se o vetor U e combinação linear (soma de múltiplos escalares) de V e W:V = (9, −12, −6), W = (−1, 7, 1) e U = (−4, −6, 2);V = (5, 4, −3), W = (2, 1, 1) e U = (−3, −4, 1).
Verifique se é um paralelogramo o quadrilátero de vértices (não necessariamente consecutivos):A = (4, −1, 1), B = (9, −4, 2), C = (4, 3, 4) e D = (4, −21, −14)A = (4, −1, 1), B = (9, −4, 2), C = (4, 3
Verifique se os pontos dados a seguir são colineares, isto e, pertencem a uma mesma reta:A = (5, 1, −3), B = (0, 3, 4) e C = (0, 3, −5);A = (−1, 1, 3), B = (4, 2, −3) e C = (14, 4, −15).
Verifique se os pontos dados a seguir são colineares, isto e, pertencem a uma mesma reta:A = (5, 1, −3), B = (0, 3, 4) e C = (0, 3, −5);A = (−1, 1, 3), B = (4, 2, −3) e C = (14, 4, −15).