Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 19b

Dado o triângulo da Figura 5-8, sejam a = | | C B → | | e b = | | C A → | | suponhamos que a ≠ b . Seja Y a intersecção da reta AB com a bissetriz do ângulo externo do vértice C.

b) Exprima C Y → em função de C A → ,   C B → ,   a ,   b . Exprima A Y → em função de A B → ,   a ,   b .

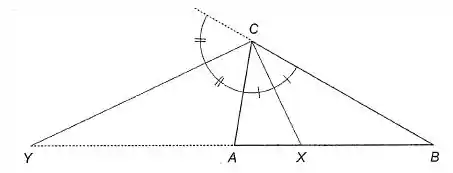
Passo 1

Vamos começar melhorando isso aqui, ok?

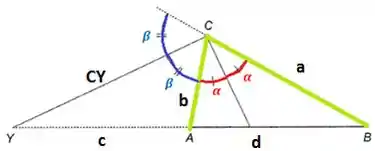
Pelo teorema da bissetriz interna, nós temos que:

a c + d = b c         →         a b = c + d c = 1 + d c

a - b b = d c

Usando a matemática vetorial nós vamos descobrir que:

B A → = a - b b A Y →

Podemos reescrever:

C A → + A Y → = C Y →

Substituindo A Y → :

C A → + b a - b B A → = C Y →

C Y → = a - b C A → + b B A → a - b

Rescrevendo B A → = C A → - C B → :

C Y → = a - b C A → + b C A → - C B → a - b

C Y → = a C A → - b C A → + b C A → - b C B → a - b

C Y → = a C A → - b C B → a - b

Portanto, podemos dizer que:

C Y → = a a - b C A → - b a - b C B →

E finalizamos mais umaa !!

Resposta

C o m o   v i s t o   a c i m a     ‼

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que se α V = 0 - , então α = 0 ou V = 0 - .
Mostre que se α V = 0 - , então α = 0 ou V = 0 - .
Se α U = α V , então U = V ? E se α ≠ 0 ?
Sejam A ,B e C pontos quaisquer com A ≠ B . Prove que:c) Um ponto X é um ponto interior ao triângulo A B C ( A ' X → = λ A ' B ' → ,c o m0λ1 , em que A ' é um ponto interior ao segmento A C e B ' é in
Sejam A ,B e C pontos quaisquer com A ≠ B . Prove que:a) Um ponto X pertence a reta determinada por A e B ( A X → = λ A B → ) se, e somente se, C X → = α C A → + β C B → com α + β = 1 .