Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 11
(a) Dado o triângulo , sejam , e pontos tais que , e . Exprima , e em função de e , e prove que existe um triângulo de lados paralelos a , e .
(b) Dado o triângulo , sejam , e tais que , e , com , e em . Prove que existe um triângulo de lados paralelos e congruentes a , e se, e somente se, .
Passo 1
Vamos seguir a dica do enunciado: começamos exprimindo , e em função de e .
Para isso vamos fazer um esboço dos segmentos que aparecem no enunciado. Primeiro desenhamos , e em qualquer lugar:
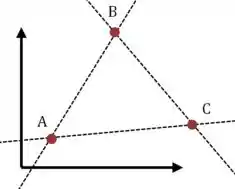
E depois colocamos os pontos , e de acordo com as fórmulas do enunciado, que dizem quais segmentos são paralelos:
Então:
Beleza, isso vai ajudar a escrever as expressões.
Passo 2
Olhando para o desenho, vamos procurar em função de e .
O jeito mais fácil de escrever seria:
Só que a gente não tem nenhum desses segmentos no enunciado. Precisamos reescrever. Podemos encontrar invertendo o sinal de :
E podemos encontrar com essa expressão que podemos extrair do desenho:
Mas o enunciado diz que :
Substituindo isso na expressão de :
Mas o enunciado sugeriu escrevermos em função de , então vamos inverter o sinal desse último também:
Ok, vamos em frente.
Passo 3
Agora vamos procurar nesses mesmos termos.
Olhando de novo para o desenho:
Trocando o sinal do primeiro termo para obter :
E substituindo com :
Passo 4
A fazendo a mesma coisa para :
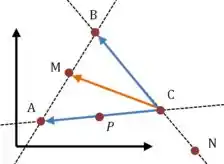
Podemos entender isso como uma soma vetorial, usando a regra do paralelogramo:
Ou seja, ficamos com:
O enunciado pediu pra mostrarmos que dá pra construir um triângulo com vetores paralelos a esses. (Não disse que precisam ser congruentes!)
Se existe alguma combinação linear desses vetores, de forma que:
Então dá pra construir um triângulo com lados paralelos a esses vetores. Com exceção, claro, do caso em que .
Passo 5
Vamos chamar e :
Substituindo isso na nossa equação:
Multiplicando tudo por :
Como e são sempre diferentes de zero, a única solução é:
Esse sistema tem infinitas soluções! Então já sabemos que é possível construir o triângulo. Mas de qualquer forma vamos procurar uma solução para ter o exemplo.
Escolhendo arbitrariamente :
E subtraindo as equações:
E substituindo isso na primeira equação:
Então a solução é:
E isso dá um triângulo de lados paralelos a , e .
Passo 6
(b) Agora vamos supor que as relações entre os vetores sejam:
Qual é a condição para que exista um triângulo de lados paralelos e congruentes a , e ?
Vamos refazer nossas expressões para , e em função de e :
Substituindo mais algumas relações:
Dessa vez os lados do nosso triângulo tem que ser paralelos e congruentes a esses três vetores.
Então a condição é:
Passo 7
Substituindo com as expressões ali de cima:
Abrindo os parênteses:
Então:
Ou seja:
Que é exatamente o que queríamos provar!
Resposta
(a) Demonstração.
(b) Demonstração.