Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento geométrico - Ex. 16
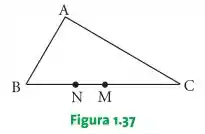
No triângulo (Figura 1.37), tem-se e . Expressar os vetores e em função de e .
Passo 1
Então galera, para conseguirmos expressar os vetores vetores e em função de e temos que fazer uma análise profunda dos vetores que compõem o triângulo . Da figura que nos foi dada conseguimos tirar algumas informações, saca só:
A primeira é que:
A segunda é que:
E como , então:
Aqui vale ressaltar que essas três expressões foram tiradas a partir de uma análise de pura soma de vetores mesmo, galera. Não tem nada de informação nova não, ok? Show! Vamos guardar essas informações, belê?
Passo 2
Agora que definimos uma expressão para , vamos substituir o que temos, se liga:
Que é o vetor escrito em função dos vetores e , como queríamos! Agora vamos para !
Passo 3
Da figura que nos foi dada conseguimos tirar que:
Mas como o enunciado nos diz que , então:
Substituindo , teremos:
Que é o vetor escrito em função dos vetores e , como queríamos!
E está aí nossa resolução, peoples!