Dados e :
Encontre vetores e que complete junto com e uma base do .
Passo 1
Para fazer isso agora é interessante se a gente pegar e escalonar a seguinte matriz cuja as linhas são dadas pelos vetores e para simplificar a nossa vida, dessa forma:
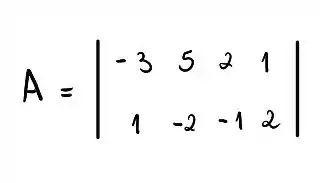
Uma vez que estamos procurando um conjunto de vetores que apenas forneça a solução trivial para a seguinte expressão:
Vamos começar a escalonar! Bora lá!
Passo 2
A primeira coisa é sempre transformar o primeiro termo da primeira coluna em 1, pois ele será nosso pivô, podemos fazer isso dividindo a primeira linha por :

Agora, precisamos eliminar os termos restantes da primeira coluna, isso pode ser feito subtraindo a linha 1 da linha 2, saca só!
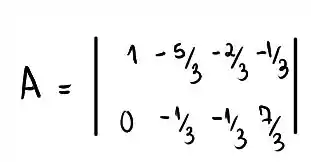
Beleza, agora precisamos transformar o segundo termo da segunda coluna em 1, podemos fazer isso multiplicando a segunda linha por , de forma que:
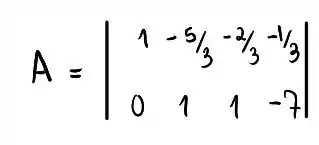
Para finalizar, vamos eliminar o termo restante da segunda coluna, para isso, podemos somar na primeira linha a segunda linha multiplicada por , obtendo:

Isso é o máximo que conseguimos simplificar este sistema, vamos procurar os nossos outros dois vetores agora!
Passo 3
Podemos dar um bom chute de vetores linearmente independentes se adicionarmos a matriz que construímos acima as seguintes linhas:

Ou seja, estamos chutando os vetores e . Note que se observamos a seguinte equação:
Como temos termos na componente e em e respectivamente, será impossível somar estes vetores e obter 0, já que termos em diferentes componentes não se somam! Portanto temos apenas a solução trivial . Sendo assim, nossos vetores são linearmente independentes e portanto formam uma base! A questão foi isso, te vejo na próxima!