Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 5.Problemas propostos - Ex. 34c

Dados o ponto A = 3,4 , - 2 e a reta x = 1 + t y = 2 - t z = 4 + 2 t

  1. Determinar o ponto simétrico de em relação à r .

Passo 1

De acordo com o item anterior sabemos o valor da altura, sendo h = 2 5 .

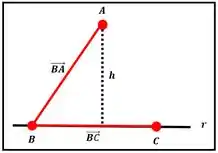
Representação dos pontos

Para determinar o simétrico precisamos conhecer o vetor que se inicia na projeção ortogonal de A sobre a reta e termina em A. Por enquanto conhecemos apenas o módulo h desse vetor.

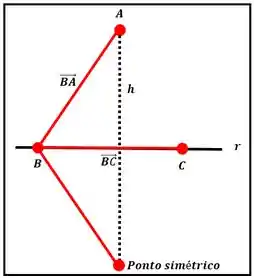
Representação da posição do ponto simétrico

Calculo da projeção

u → = p r o j B C → B A → = B A → . B C → B C → 2 B C →                                               ( e q u a ç ã o   I )

B A → . B C → = 2,2 , - 6 1 , - 1,2 = - 1 2                                               ( e q u a ç ã o   I I )

B C → = 6 2 = 6                                               ( e q u a ç ã o   I I I )

Substituindo as e q u a ç õ e   I I   e   I I I na e q u a ç ã o   I .

u → = p r o j B C → B A → = - 12 6 1 , - 1,2

u → = p r o j B C → B A → = - 2 1 , - 1,2

u → = p r o j B C → B A → = ( - 2 , 2 , - 4 )

Passo 2

Encontrando o vetor w → = p r o j B C → B A → - p r o j B C → B A → = B A → - u →

2,2 , - 6 - - 2,2 , - 4 = 4,0 , - 2

A - 2 w → = 3,4 , - 2 - 2 4,0 , - 2 = ( - 5,4 , 2 )

O ponto simétrico é P = ( - 5,4 , 2 ) .

Resposta

O ponto simétrico é P = ( - 5,4 , 2 ) .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam A = 0 ,2 ,1 e r : X = 0 ,2 ,- 2 + λ ( 1 ,- 1 ,2 ) . Obtenha os pontos de r que distam 3 de A . Em seguida verifique se a distância do ponto A à reta r é maior, menor ou igual a 3 e justifique su
Sejam P = ( 2 ,1 ,- 1 ) e Q = ( 0 ,- 1 ,0 ) . Determine um ponto C da reta P Q tal que a área do triângulo A B C seja 9 , nos casos:b) A = - 2 ,3 ,4 ,B = ( - 6 ,- 1 ,6 )
Sejam P = ( 2 ,1 ,- 1 ) e Q = ( 0 ,- 1 ,0 ) . Determine um ponto C da reta P Q tal que a área do triângulo A B C seja 9 , nos casos:d) A = 1 ,2 ,7 ,B = ( - 5 ,- 4 ,- 5 )
Sejam P = ( 2 ,1 ,- 1 ) e Q = ( 0 ,- 1 ,0 ) . Determine um ponto C da reta P Q tal que a área do triângulo A B C seja 9 , nos casos:c) A = - 1 ,1 ,2 ,B = ( - 5 ,- 3 ,4 )
Sejam P = ( 2 ,1 ,- 1 ) e Q = ( 0 ,- 1 ,0 ) . Determine um ponto C da reta P Q tal que a área do triângulo A B C seja 9 , nos casos:a) A = 0 ,3 ,0 ,B = ( 6 ,3 ,3 )