Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 5.Problemas propostos - Ex. 34b
Dados o ponto e a reta
- Calcular a distância de a .
Passo 1
Para encontrarmos a distância de a precisamos de dois pontos distintos que pertença a esta reta.
Para
Para
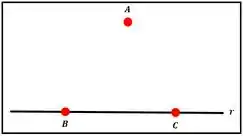
Representação dos pontos , e
Precisamos dos vetores e
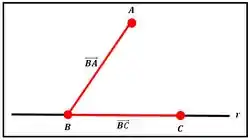
Representação dos vetores
O produto vetorial possui o módulo igual ao valor da área do paralelogramo determinado por esses vetores.
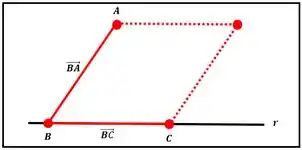
O módulo de é
A base do paralelogramo é , sendo assim, seu módulo será:
Logo determinamos a altura a partir da área do paralelogramo.
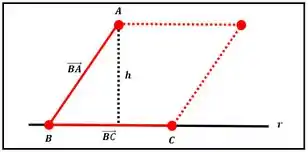
Resposta
A distância de a é .
Exercícios de Livros Relacionados
Obtenha os pontos da interseção dos planos π 1 : x + y = 2 e π 2 : x = y + z que distam 14 3 da reta s : x = y = z + 1 .
Verifique para quais pontos X da reta r a área do triângulo A B X é a menor possível e comente as peculiaridades geométricas de cada caso.a) A = 2 ,3 ,1B = 7 ,1 ,5r : X = - 4 ,6 ,1 + λ 1 ,2 ,2
Calcule a distância do ponto P à reta r .b) P = 1 ,0 ,1 , r : x = 2 y = 3 z
Verifique para quais pontos X da reta r a área do triângulo A B X é a menor possível e comente as peculiaridades geométricas de cada caso.c) A = 2 ,0 ,0B = 3 ,1 ,0r : X = 3 ,1 ,8 + λ ( 1 ,1 ,2 )
Obtenha os pontos da reta r que equidistam das retas s e t :b) r : x = y = zs : X = 1 ,0 ,0 + λ 1 ,1 ,0 t : X = 0 ,0 ,1 + λ ( 1 ,0 ,- 1 )